Ôn thi vào 10
Các câu hỏi tương tự
Cho đường tròn (O; R) đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O). Trên tia Ax lấy điểm E khác A. Vẽ tiếp tuyến EC với đường tròn (O) (E là tiếp điểm, C khác A). a) CM: 4 điểm A, E, C, O cùng thuộc một đường tròn.b) Gọi K là trung điểm của BC. Tia OK cắt tia EC tại F. Chứng minh BF là tiếp tuyến của đường tròn (O).c) Gọi H là giao điểm của AC và OE. Chứng minh AB^24OH.OE
Đọc tiếp
Cho đường tròn (O; R) đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O). Trên tia Ax lấy điểm E khác A. Vẽ tiếp tuyến EC với đường tròn (O) (E là tiếp điểm, C khác A). a) CM: 4 điểm A, E, C, O cùng thuộc một đường tròn.b) Gọi K là trung điểm của BC. Tia OK cắt tia EC tại F. Chứng minh BF là tiếp tuyến của đường tròn (O).c) Gọi H là giao điểm của AC và OE. Chứng minh \(AB^2=4OH.OE\)
cho đường tròn (o,r) có dây B,C ko đi qua tâm. từ điểm A thuộc tia đối của tia BC, vẽ các tiếp tuyến AE, AF của đường tròn O với E,F là các tiếp điểm. gọi I là trung điểm của BC, D là giao điểm thứ 2 của FI và (O), H là giao điểm của EF và AC. chứng minh: a) ED//ACb) AH.AI AB.ACgiúp mình câu b thôi
Đọc tiếp
cho đường tròn (o,r) có dây B,C ko đi qua tâm. từ điểm A thuộc tia đối của tia BC, vẽ các tiếp tuyến AE, AF của đường tròn O với E,F là các tiếp điểm. gọi I là trung điểm của BC, D là giao điểm thứ 2 của FI và (O), H là giao điểm của EF và AC. chứng minh:
a) ED//AC
b) AH.AI = AB.AC
giúp mình câu b thôi 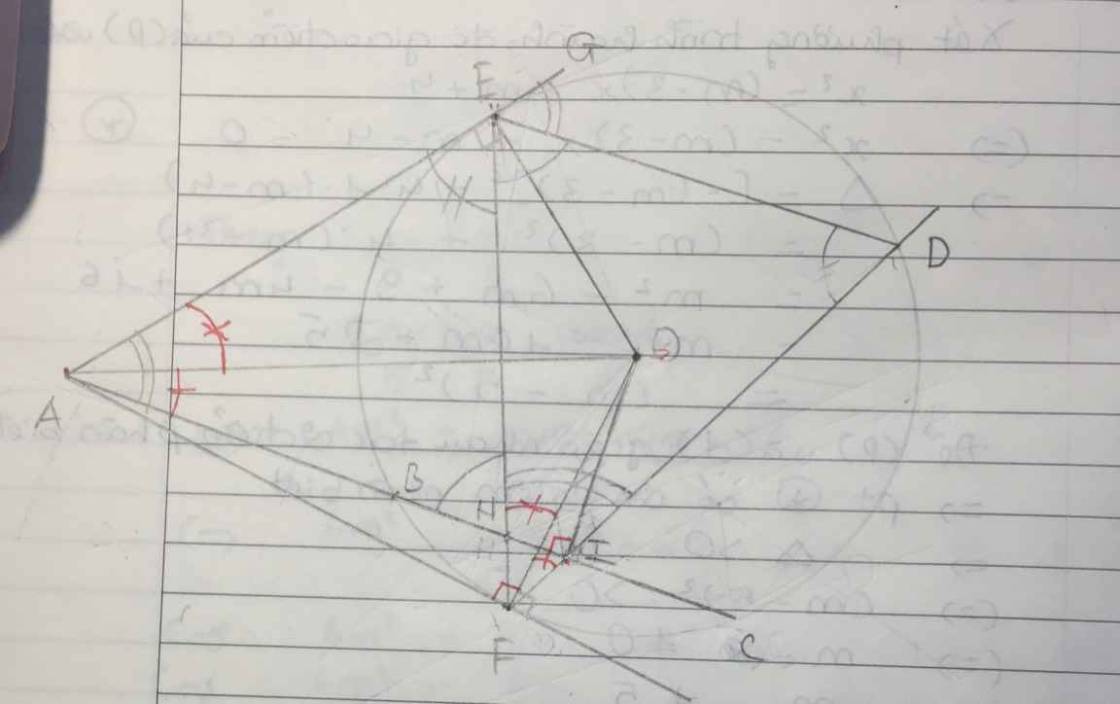
Cho đường tròn (O;R) có 2 đường kính AB vuông góc với CD .Trên đoạn thẳng AO lấy điểm M .Tia CM cắt (O;R) tại điểm thứ 2 là N .kẻ tiếp tuyến với (O;R) tại N .Tiếp tuyến này cắt đường thẳng vuông góc với AB tại M ở P a, c/m :OMNP là tứ giác nội tiếp b, c/m : CN//OP
Cho đường tròn (O;R) và điểm A nằm ngoài đường tròn. Qua A kẻ 2 tiếp tuyến AB, AC với đường tròn (B,C là các tiếp điểm)
a) Chứng minh: 4 điểm A,B,O,C cùng thuộc một đường tròn
b) Kẻ cát tuyến ADE nằm giữa AO và AB (D nằm giữa A và E), kẻ các tiếp tuyến tại D và E cắt nhau tại S. Nối BC cắt OA tại H. Chứng minh: R^2=OH.OA và 3 điểm S, B,C thẳng hàng
Từ một điểm A nằm ngoài đường tròn tâm O, bán kính R (AO 2R) vẽ hai tiếp tuyến AD, AE với (O) (D,E là các tiếp điểm).Gọi H là giao điểm của DE và AO.Lấy điểm M thuộc cung nhỏ DE (M khác D khác E, MD ME).Tia AM cắt đường tròn (O;R) tại N.Đoạn thẳng AO cắt cung nhỏ DE tại K.a) Chứng minh AO vuông góc với DE và AD2 AM.ANb) Chứng minh NK là tia phân giác của góc DNI và tứ giác MHON nội tiếp.c) Kẻ đường kính KQ của đường tròn (O;R).Tia QN cắt tia ED tại C.Chứng minh MD.CE ME.CD
Đọc tiếp
Từ một điểm A nằm ngoài đường tròn tâm O, bán kính R (AO < 2R) vẽ hai tiếp tuyến AD, AE với (O) (D,E là các tiếp điểm).Gọi H là giao điểm của DE và AO.Lấy điểm M thuộc cung nhỏ DE (M khác D khác E, MD < ME).Tia AM cắt đường tròn (O;R) tại N.Đoạn thẳng AO cắt cung nhỏ DE tại K.
a) Chứng minh AO vuông góc với DE và AD2 = AM.AN
b) Chứng minh NK là tia phân giác của góc DNI và tứ giác MHON nội tiếp.
c) Kẻ đường kính KQ của đường tròn (O;R).Tia QN cắt tia ED tại C.Chứng minh MD.CE = ME.CD
1 cho đường tròn tâm O có đường kính AB và điểm C thuộc đường tròn đó (C khác A, B). Lấy điểm D thuộc dây BC tại điểm E, tia AC cắt tia BE tại điểm F
a, cmr FCDE là tứ giác nội tiếp đường tròn
b, cmr DA . DE = DB . DC
c, gọi I là tâm của đường tròn ngoại tiếp tam giác FCDE, cmr IC là tiếp tuyến
Cho đường tròn (O;R) có đường kính BC. Trên tia đối của tia BC lấy cung DE của đường tròn (O) vuông góc với BCa) AE là tiếp tuyến của đường tròn (O)b) Vẽ đường kính DF của đường tròn (O). Gọi P là giao điểm của EC và DF, G là giao điểm của 2 đường thẳng BD và AE. Chứng minh BC//EF và PO.GEPC.GBc) Vẽ cát tuyến AMN của đường tròn (O) ( cát tuyến không đi qua O ), các tuyến tại M và N của đường tròn (O) cắt nhau tại K. Chứng minh ba điểm K,D,E thẳng hàng.
Đọc tiếp
Cho đường tròn (O;R) có đường kính BC. Trên tia đối của tia BC lấy cung DE của đường tròn (O) vuông góc với BC
a) AE là tiếp tuyến của đường tròn (O)
b) Vẽ đường kính DF của đường tròn (O). Gọi P là giao điểm của EC và DF, G là giao điểm của 2 đường thẳng BD và AE. Chứng minh BC//EF và PO.GE=PC.GB
c) Vẽ cát tuyến AMN của đường tròn (O) ( cát tuyến không đi qua O ), các tuyến tại M và N của đường tròn (O) cắt nhau tại K. Chứng minh ba điểm K,D,E thẳng hàng.
Cho đường tròn \(\left(O;AB=2R\right)\). Lấy C là một điểm trên đường tròn để \(AC>BC\). Vẽ hình vuông ACDE có D thuộc tia tia đối của tia BC. CE cắt đường tròn tại F (F không trùng C). Qua A, kẻ tiếp tuyến cắt BF tại H. Chứng minh rằng D, E, H thẳng hàng.
*Giải bằng cách xét 2 tam giác AEH và ACB
từ một điểm A nằm ngoài đường tròn (O;R), kẻ 2 tiếp tuyến AB, AC với (O;R)(B và C là tiếp điểm). Vẽ đường kính BD a) chứng minh AO vuông góc BC tại H và CD song song OA b)AD cắt đường tròn tại K. chứng minh AD.AK=AH.AO












