Question

* Cho đoạn thẳng AB=2a. Từ trung điểm O của AB vẽ tia Ox⊥AB. Trên Ox, lấy điểm D sao cho OD=\(\dfrac{a}{2}\). Từ B kẽ BC vuông góc với đường thẳng AD.

a. Tính AD, AC và BC theo a

b. Kéo dài DO một đoạn OE=a. Chứng minh bốn điểm A,B,C và E cùng nằm trên một đường tròn

Answer 1

Answer 2

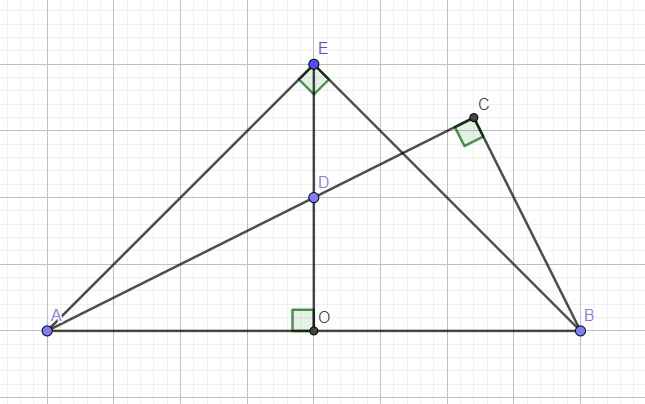
O là trung điểm AB \(\Rightarrow OA=OB=\dfrac{AB}{2}=a\)

Áp dụng định lý Pitago:

\(AD=\sqrt{AO^2+OD^2}=\dfrac{a\sqrt{5}}{2}\)

Xét hai tam giác vuông AOD và ACB có góc A chung

\(\Rightarrow\Delta AOD\sim\Delta ACB\Rightarrow\dfrac{AD}{AB}=\dfrac{AO}{AC}\Rightarrow AC=\dfrac{AO.AB}{AD}=\dfrac{4a\sqrt{5}}{5}\) 

\(BC=\sqrt{AB^2-AC^2}=\dfrac{2a\sqrt{5}}{5}\)

b. Ta có: \(AE=\sqrt{AO^2+OE^2}=a\sqrt{2}\)

\(BE=\sqrt{OB^2+OE^2}=a\sqrt{2}\)

\(\Rightarrow AE^2+BE^2=4a^2=AB^2\)

\(\Rightarrow\Delta ABE\) vuông tại E (Pitago đảo)

\(\Rightarrow\) Hai điểm E và C cùng nhìn AB dưới 1 góc vuông nên bốn điểm A,B,C,E cùng thuộc đường tròn đường kính AB (đpcm)