Cho biểu thức
K= x + √x / x+√x+1 - [√x (2x + √x-1)/ x\(\sqrt[]{x}\) -1) + \(\dfrac{1}{1-\sqrt{ }x}\)] : (\(\dfrac{\sqrt{x}-1}{\sqrt{ }x}\)- \(\dfrac{\sqrt{x}}{\sqrt{ }x-1}\))
a) tìm điều kiện để biểu thức xác định
b) rút gọn biểu thức
c) tìm giá trị của x để K=\(\dfrac{1}{3}\)
d) tính giá trị của K khi x= 5-2\(\sqrt{6}\). hãy trục căn thức ở mẫu của kết quả tìm đc
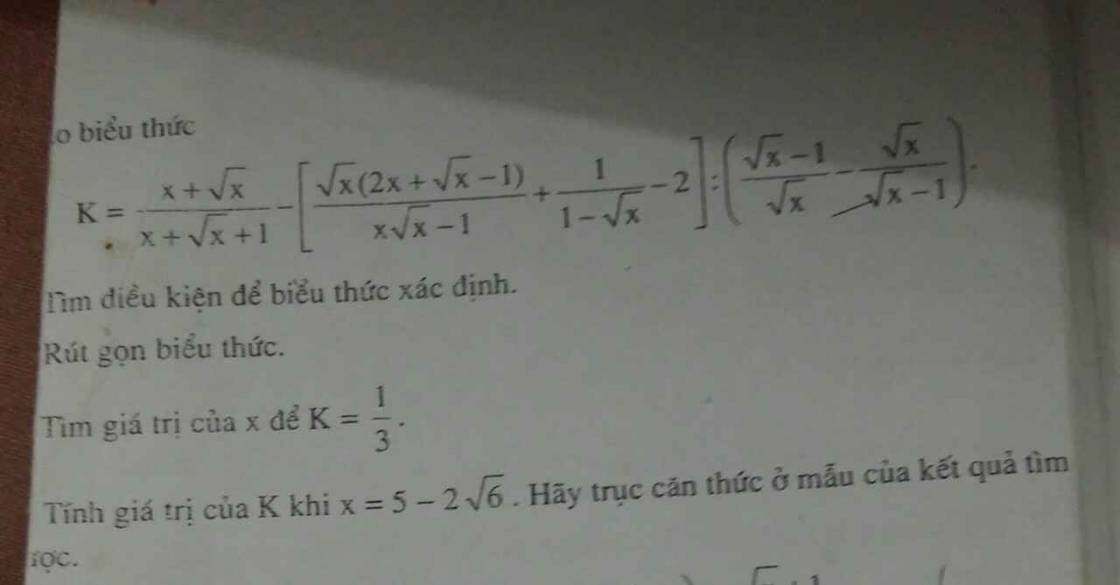 | |
a, đk x > 0 ; x khác 1
\(K=\dfrac{x+\sqrt{x}}{x+\sqrt{x}+1}-\left(\dfrac{2x\sqrt{x}+x-\sqrt{x}-x-\sqrt{x}-1-2x\sqrt{x}+2}{x\sqrt{x}-1}\right):\left(\dfrac{x-2\sqrt{x}+1-x}{x-\sqrt{x}}\right)\)
\(=\dfrac{x+\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{-2\sqrt{x}+1}{x\sqrt{x}-1}:\dfrac{-2\sqrt{x}+1}{x-\sqrt{x}}=\dfrac{x+\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{\sqrt{x}}{x+\sqrt{x}+1}=\dfrac{x}{x+\sqrt{x}+1}\)
b, Ta có \(K=\dfrac{x}{x+\sqrt{x}+1}=\dfrac{1}{3}\Leftrightarrow3x=x+\sqrt{x}+1\Leftrightarrow2x-\sqrt{x}-1=0\Leftrightarrow\left(\sqrt{x}-1\right)\left(2\sqrt{x}+1\right)=0\Leftrightarrow x=1\)
c, bạn tự làm nhé














