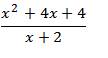Question

Cho B= \(\dfrac{x+2}{2\text{x}-4}+\dfrac{x-2}{2\text{x}+4}+\dfrac{-8}{x^2-4}\)

a, Tìm điều kiện của B để B là phân thức xác định

b, Rút gọn B

c, Tìm giá trị nguyên của x để B có giá trị nguyên

Answer 1

a. Điều kiện xác định của B là x\(\ne\)2; x\(\ne\)-2

b. B= \(\dfrac{x+2}{2x-4}\)+\(\dfrac{x-2}{2x+4}\)+\(\dfrac{-8}{x^2-4}\)=\(\dfrac{\left(x+2\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}\)+\(\dfrac{\left(x-2\right)\left(x-2\right)}{2\left(x+2\right)\left(x-2\right)}\)+\(\dfrac{-8\cdot2}{2\left(x-2\right)\left(x+2\right)}\)=\(\dfrac{x^2+4x+4+x^2-4x+4-16}{2\left(x+2\right)\left(x-2\right)}\)=\(\dfrac{2x^2-8}{2\left(x+2\right)\left(x-2\right)}\)=\(\dfrac{2\left(x^2-4\right)}{2\left(x-2\right)\left(x+2\right)}\)=\(\dfrac{2\left(x-2\right)\left(x+2\right)}{2\left(x-2\right)\left(x+2\right)}\)=1