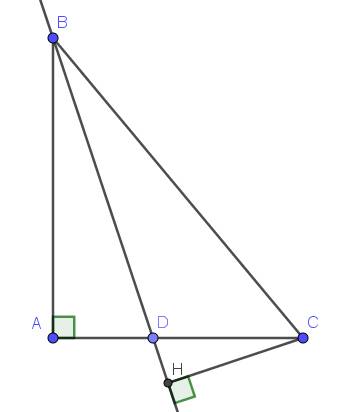
a: \(AC=\sqrt{20^2-16^2}=12\left(cm\right)\)
BD là phân giác
=>AD/AB=CD/BC
=>AD/4=CD/5=(AD+CD)/(4+5)=12/9=4/3
=>AD=16/3cm; CD=20/3cm
b: Xét ΔABD vuông tại A và ΔHCD vuông tại H có
góc ADB=góc HDC
=>ΔABD đồng dạng với ΔHCD
Lời giải:
a.
Áp dụng định lý Pitago:
$AC=\sqrt{BC^2-AB^2}=\sqrt{20^2-16^2}=12$ (cm)
Áp dụng tính chất tia phân giác:
$\frac{AD}{CD}=\frac{AB}{BC}=\frac{16}{20}=\frac{4}{5}$
$\Rightarrow \frac{AD}{AD+CD}=\frac{4}{9}$
$\Rightarrow \frac{AD}{AC}=\frac{4}{9}\Rightarrow AD=\frac{4}{9}AC=\frac{4}{9}.12=\frac{16}{3}$ (cm)
$CD=AC-AD=12-\frac{16}{3}=\frac{20}{3}$ (cm)
b.
Xét tam giác $ABD$ và $HCD$ có:
$\widehat{BAD}=\widehat{CHD}=90^0$
$\widehat{BDA}=\widehat{CDH}$ (đối đỉnh)
$\Rightarrow \triangle ABD\sim \triangle HCD$ (g.g)
c.
Từ kết quả tam giác đồng dạng phần b suy ra:
$\frac{S_{HCD}}{S_{ABD}}=(\frac{CD}{BD})^2(*)$
Trong đó:
$CD=\frac{20}{3}$
$BD=\sqrt{AB^2+AD^2}=\sqrt{16^2+(\frac{16}{3})^2}=\frac{16\sqrt{10}}{3}(**)$
Từ $(*); (**)\Rightarrow \frac{S_{HCD}}{S_{ABD}}=\frac{5}{32}$
$\Rightarrow S_{HCD}=\frac{5}{32}S_{ABD}=\frac{5}{32}.\frac{AD}{AC}S_{ABC}$
$=\frac{5}{32}.\frac{16}{3.12}.\frac{AB.AC}{2}$
$=\frac{5}{32}.\frac{4}{9}.\frac{16.12}{2}=\frac{20}{3}$ (cm2)