`a,`
Ta có: \(\left\{{}\begin{matrix}\text{BE }\bot\text{ Ax}\\\text{CF }\bot\text{ Ax}\end{matrix}\right.\)
`@` Theo tiên đề Euclid
`-> \text {BE // CF}`
`b,`
Xét `2 \Delta` vuông `BEM` và `CFM`:
`\text {MB = MC (M là trung điểm của BC)}`
$\widehat {BME} = \widehat {CMF} (\text {2 góc đối đỉnh})$
`=> \Delta BEM = \Delta CFM (ch-gn)`
`c,`
Vì `\Delta BEM = \Delta CFM (b)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
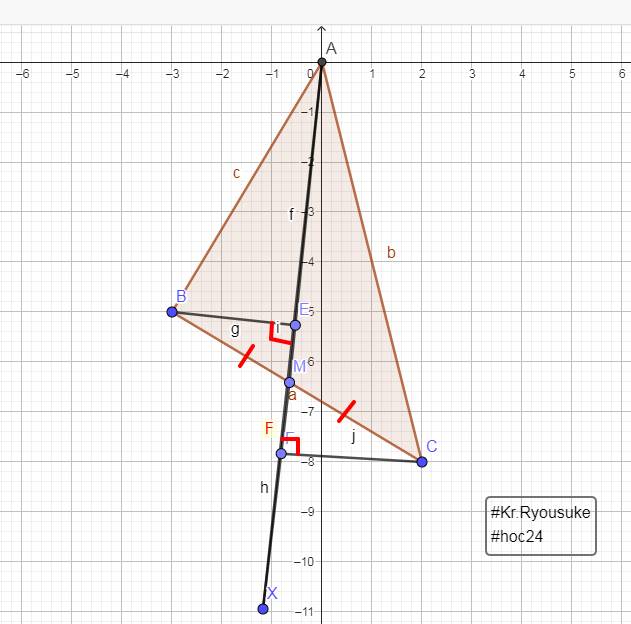
a:BE vuông góc AM
CF vuông góc AM
=>BE//CF
b: Xet ΔBEM vuông tại E và ΔCFM vuông tại F có
MB=MC
góc BME=góc CMF
=>ΔBEM=ΔCFM
b: ΔBEM=ΔCFM
=>BE=CF












