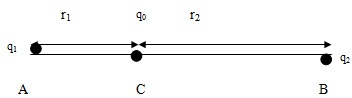
(Cái hình này toi lấy trên gg, thay \(q_0\) là \(q_3\) nha)
\(q_1=q_2=4q\)
\(\Rightarrow q_1;q_2\) cùng dấu
Để \(q_3\) nằm cân bằng thì \(\overrightarrow{F_{13}}+\overrightarrow{F_{23}}=0\) (với \(F_{13};F_{23}\) là lực do \(q_1;q_2\) tác dụng lên \(q_3\))
\(\Rightarrow\)\(q_3\) nằm trên đường thẳng nối \(q_1;q_2\)
Có: \(\left\{{}\begin{matrix}F_{13}=F_{23}\\r_1+r_2=AB\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}k.\dfrac{\left|q_1.q_3\right|}{r_1^2}=k.\dfrac{\left|q_2.q_3\right|}{r_2^2}\\r_1+r_2=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{r_1}{r_2}=\sqrt{\dfrac{\left|q_1\right|}{\left|q_2\right|}}=1\\r_1+r_2=2\end{matrix}\right.\)\(\Rightarrow r_1=r_2=1\)
Vậy \(q_3\) nằm ở vị trí trung điểm của AB











