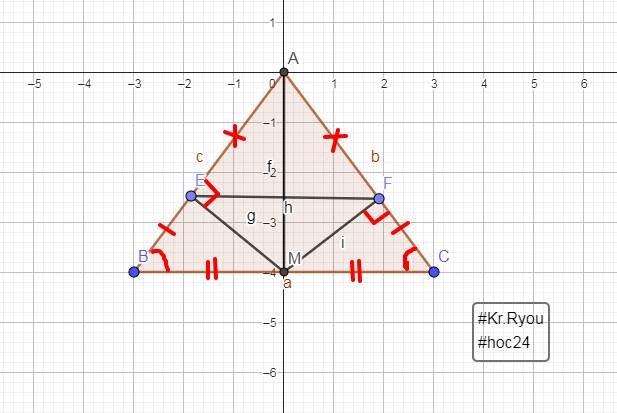
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>ME=MF và AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
`@` `\text {Ans}`
`\downarrow`
`a,`
Xét `\Delta ABM` và `\Delta ACM:`
\(\text{AB = AC (}\Delta\text{ABC cân tại A)}\)
\(\widehat{\text{ABC}}=\widehat{\text{ACB}}\left(\Delta\text{ABC cân tại A}\right)\)
\(\text{MB = MC (trung tuyến AM)}\)
`=> \Delta ABM = \Delta ACM (c-g-c)`
`b,`
Xét `\Delta BEM` và `\Delta CFM`:
`\text {MB = MC (trung tuyến AM)}`
$\widehat {MBE} = \widehat {MCF} (\Delta \text {ABC cân tại A})$
\(\widehat {BEM} = \widehat {CFM} (=90^0)\)
`=> \Delta BEM = \Delta CFM (ch-gn)`
`=> \text {ME = MF (2 cạnh tương ứng)}`
`c,`
Vì `\Delta BEM = \Delta CFM (b)`
`=> \text {BE = CF (2 cạnh tương ứng)}`
Ta có: \(\left\{{}\begin{matrix}\text{AB = AE + BE }\\\text{AC = AF + CF}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\text{AB = AC}\\\text{BE = CF}\end{matrix}\right.\)
`=> \text {AE = AF}`
Xét `\Delta AEF`:
`\text {AE = AF}`
`=> \Delta AEF` cân tại A
`=>` \(\widehat{\text{AEF}}=\widehat{\text{AFE}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(1)`
`\Delta ABC` cân tại A
`=>`\(\widehat{\text{ABC}}=\widehat{\text{ACB}}=\dfrac{180^0-\widehat{\text{A}}}{2}\) `(2)`
Từ `(1)` và `(2)`
`=>`\(\widehat{\text{AEF}}=\widehat{\text{ABC}}\)
Mà `2` góc này nằm ở vị trí đồng vị
`=> \text {EF // BC (tính chất 2 đường thẳng song song)}`
`@` `\text {Kaizuu lv uuu}`