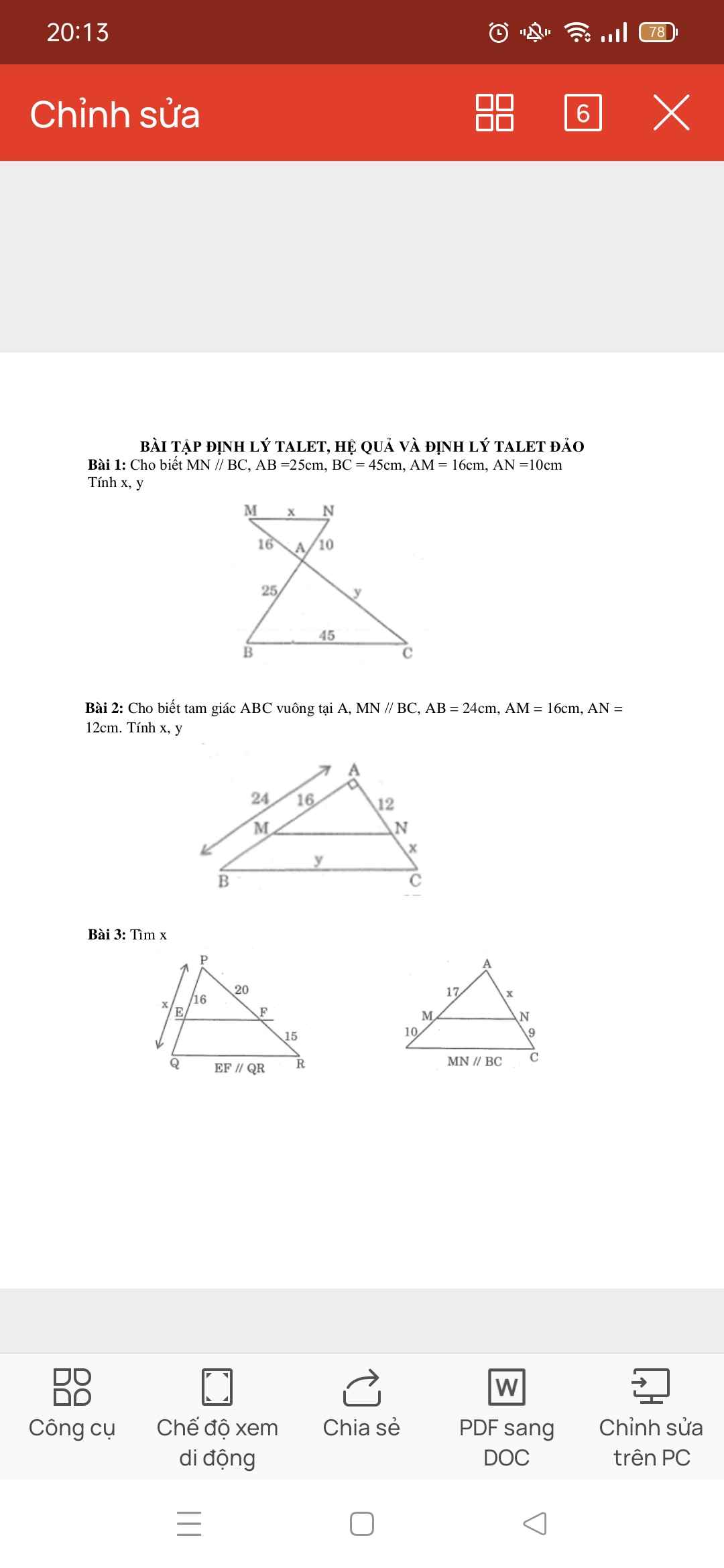
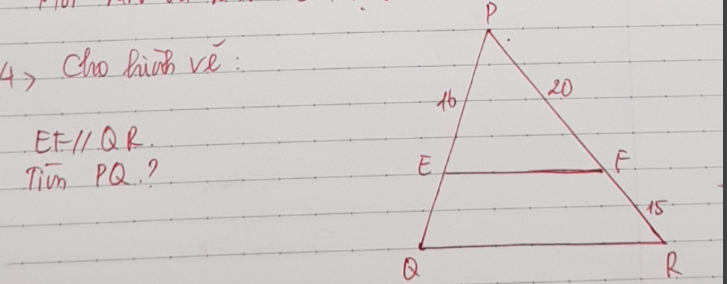
a: Xét ΔKAB và ΔKCD có
\(\widehat{KAB}=\widehat{KCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AKB}=\widehat{CKD}\)(hai góc đối đỉnh)
Do đó: ΔKAB đồng dạng với ΔKCD
=>\(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(KA\cdot KD=KB\cdot KC\)
b: Ta có: \(\dfrac{KA}{KC}=\dfrac{KB}{KD}\)
=>\(\dfrac{KC}{KA}=\dfrac{KD}{KB}\)
=>\(\dfrac{KC}{KA}+1=\dfrac{KD}{KB}+1\)
=>\(\dfrac{KC+KA}{KA}=\dfrac{KD+KB}{KB}\)
=>\(\dfrac{AC}{KA}=\dfrac{BD}{KB}\)
=>\(\dfrac{AK}{AC}=\dfrac{BK}{BD}\left(1\right)\)
Xét ΔADC có IK//DC
nên \(\dfrac{AK}{AC}=\dfrac{IK}{DC}\left(2\right)\)
Xét ΔBDC có KQ//DC
nên \(\dfrac{KQ}{DC}=\dfrac{BK}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra IK=KQ