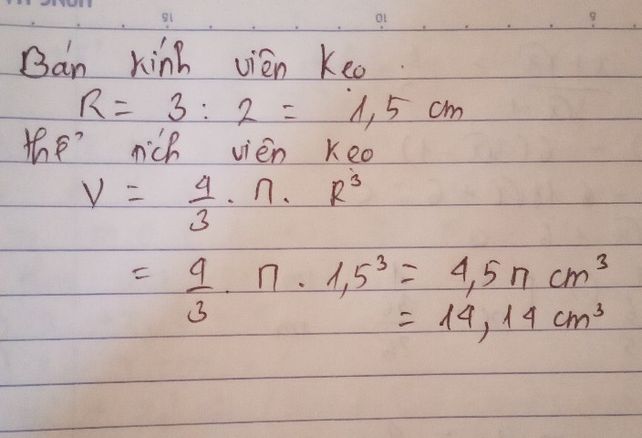Câu 1:
Cho các biểu thức A = \(\dfrac{x+3}{x-9}+\dfrac{2}{\sqrt{x}+3}\) và B = \(\dfrac{1}{\sqrt{x}-3}\), với x ≥ 0, x ≠ 9.
a) Tính giá trị của B khi x = 16;
b) Rút gọn biểu thức M = A - B;
c) Tìm x để M = \(\dfrac{\sqrt{x}+1}{\sqrt{x}+2}.\)
Câu 2:
a) Tính thể tích một viên kẹo sô-cô-la hình cầu có đường kính bằng 3cm.
b) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hai tổ sản xuất cùng làm chung một công việc thì sau 12 giờ xong. Nếu tổ 1 làm một mình trong 2 giờ, tổ 2 làm một mình trong 7 giờ thì cả hai tổ làm xong một nửa công việc. Tính thời gian mỗi tổ làm một mình xong toàn bộ công việc.
Câu 3:
1. Cho phương trình \(x-\left(m+3\right)\sqrt{x}+m+2=0\left(1\right)\)
a) Giải phương trình (1) khi m = - 4
b) Tìm m để phương trình (1) có hai nghiệm phân biệt.
2. Cho đường thẳng (d): y = (m - 1) + 4 (m ≠ 1). Đường thẳng (d) cắt Ox tại A, cắt Oy tại B. Tìm m để diện tích tam giác OAB bằng 2.
Câu 4:
Cho tam giác đều ABC nội tiếp đường tròn (O; R). Điểm M trên cung nhỏ AC. Hạ BK ⊥ AM tại K. Đường thẳng BK cắt tia CM tại E. Nối BE cắt đường tròn (O: R) tại N (N ≠ B).
a) Chứng minh tam giác MBE cân tại M;
b) Chứng minh EN.EB = EM.EC;
c) Tìm vị trí của M để tam giác MBE có chu vi lớn nhất.
Câu 5:
Giải hệ phương trình: \(\left\{{}\begin{matrix}y+xy^2=6x^2\\1+x^2y^2=5x^2\end{matrix}\right.\)
Chúc các em ôn thi tốt!
Câu 1:
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
a) Thay x=16 vào B, ta được:
\(B=\dfrac{1}{\sqrt{16}-3}=\dfrac{1}{4-3}=1\)
Vậy: Khi x=16 thì B=1
b) Ta có: M=A-B
\(=\dfrac{x+3}{x-9}+\dfrac{2}{\sqrt{x}+3}-\dfrac{1}{\sqrt{x}-3}\)
\(=\dfrac{x+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}+\dfrac{2\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}+3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x+3+2\sqrt{x}-6-\sqrt{x}-3}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+3\sqrt{x}-2\sqrt{x}-6}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)-2\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}-3}\)
c) Để \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\) thì \(\dfrac{\sqrt{x}-2}{\sqrt{x}-3}=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)=\left(\sqrt{x}-3\right)\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow x-4=x-2\sqrt{x}-3\)
\(\Leftrightarrow-2\sqrt{x}-3=-4\)
\(\Leftrightarrow-2\sqrt{x}=-1\)
\(\Leftrightarrow\sqrt{x}=\dfrac{1}{2}\)
hay \(x=\dfrac{1}{4}\)(thỏa ĐK)
Vậy: Để \(M=\dfrac{\sqrt{x}+1}{\sqrt{x}+2}\) thì \(x=\dfrac{1}{4}\)
Câu 2:
b) Gọi thời gian tổ 1 hoàn thành công việc khi làm một mình là x(giờ)
thời gian tổ 2 hoàn thành công việc khi làm một mình là y(giờ)
(Điều kiện: x>12; y>12)
Trong 1 giờ, tổ 1 làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, tổ 2 làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai tổ làm được: \(\dfrac{1}{12}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\)(1)
Vì khi tổ 1 làm trong 2 giờ, tổ 2 làm trong 7 giờ thì hai tổ hoàn thành được một nửa công việc nên ta có phương trình: \(\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{6}\\\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-5}{y}=\dfrac{-1}{3}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=15\\\dfrac{1}{x}+\dfrac{1}{15}=\dfrac{1}{12}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{60}\\y=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=60\\y=15\end{matrix}\right.\)(thỏa ĐK)
Vậy: Tổ 1 cần 60 giờ để hoàn thành công việc khi làm một mình
Tổ 2 cần 15 giờ để hoàn thành công việc khi làm một mình
Câu 2:
b)
Gọi thời gian tổ 1 làm xong công việc một mình là:x(h)
thời gian tổ 2 làm xong công việc một mình là: y(h)
Một giờ tổ 1 làm được:\(\dfrac{1}{x}\)( công việc)
Một giờ tổ 2 làm được: \(\dfrac{1}{y}\)( công việc)
Một giờ cả 2 tổ làm được: \(\dfrac{1}{12}\)( công việc )
Ta có phương trình: \(\dfrac{1}{x}\)+\(\dfrac{1}{y}\)=\(\dfrac{1}{12}\)(1)
Hai giờ tổ 1 làm được: \(\dfrac{2}{x}\)
Bảy giờ tổ 2 làm được: \(\dfrac{7}{y}\)
Cả 2 làm được nửa công việc là: \(\dfrac{1}{2}\)(2)
Từ(1) và(2) ta có hệ phương trình:
\((\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\)=>\(\dfrac{2}{x}+\dfrac{2}{y}=\dfrac{1}{6}\)=>\(\dfrac{2}{x}+\dfrac{2}{y}-\dfrac{2}{x}-\dfrac{7}{y}=\dfrac{1}{6}-\dfrac{1}{2}\)=>\(\dfrac{5}{y}=\dfrac{1}{3}\)=>y=15
\((\dfrac{2}{x}+\dfrac{7}{x}=\dfrac{1}{2}\)=>\(\dfrac{2}{x}+\dfrac{7}{y}=\dfrac{1}{2}\)=>\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\)=>x=60
Câu 1:
ĐKXĐ: {x≥0x≠9{x≥0x≠9
a) Thay x=16 vào B, ta được:
=x+3x−9+2√x+3−1√x−3=x+3x−9+2x+3−1x−3
=x+3+2√x−6−√x−3(√x+3)(√x−3)=x+3+2x−6−x−3(x+3)(x−3)
=x+3√x−2√x−6(√x+3)(√x−3)=x+3x−2x−6(x+3)(x−3)
=(√x+3)(√x−2)(√x+3)(√x−3)=(x+3)(x−2)(x+3)(x−3)
M=√x+1√x+2M=x+1x+2 thì ⇔√x=12⇔x=12
hay M=√x+1√x+2M=x+1x+2 thì 1x1x(công việc)
Trong 1 giờ, tổ 2 làm được: 112112(công việc)
Do đó, ta có phương trình: 2x+7y=122x+7y=12(2)
Từ (1) và (2) ta lập được hệ phương trình:
⇔⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩−5y=−131x+1y=112⇔⎧⎨⎩y=151x+115=112⇔{−5y=−131x+1y=112⇔{y=151x+115=112