trong △DEF có:
EM là đường trung tuyến thứ nhất
FN là đường trung tuyến thứ hai
mà hai đường này cắt nhau tại I
=> I là trọng tâm của △DEF
=>IM = 1/3 IE
=>IM/IE = 1/3
trong △DEF có:
EM là đường trung tuyến thứ nhất
FN là đường trung tuyến thứ hai
mà hai đường này cắt nhau tại I
=> I là trọng tâm của △DEF
=>IM = 1/3 IE
=>IM/IE = 1/3
mọi người làm giúp mình với mình cần gấp nha ( mong mọi ng đọc dc :)) )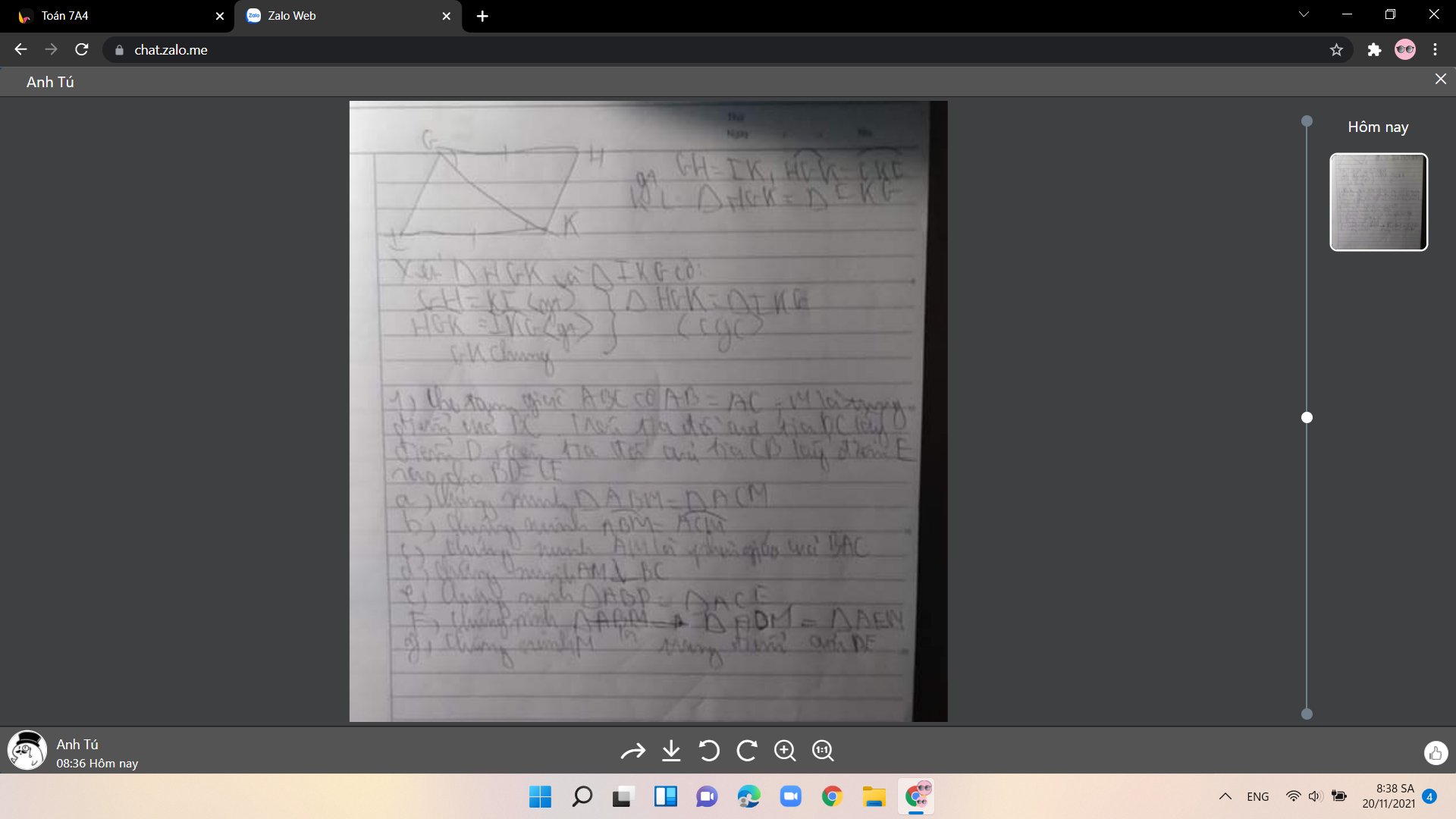
mọi người giúp mình với, mình đang cần gấp 
giải giúp mình nha mọi người
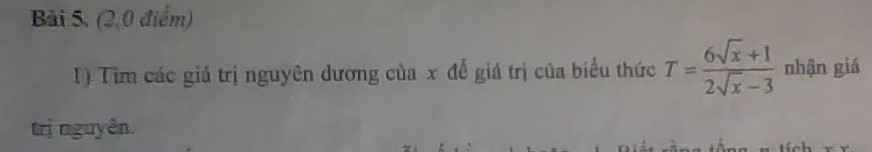
Mọi người giúp mình nha!
cho ▲ABC vuông tại A có AB = 12cm, AC = 9cm. Trên tia đối của AC lấy D sao cho AD = AC. Trên cạnh AB lấy E sao cho EA = 4cm, đường thẳng CE cắt BD tại I.
a/ Tính BC.
b/ So sánh các góc của ▲ABC.
c/ Cm: ▲BDC là tam giác cân.
d/ Cm: CI là đường trung tuyến của tam giác BDC.
Mình chỉ cần trình bày câu d thôi mọi người giúp mình nha
Cho tam giác ABC vuông tại A, AB<AC.Đường trung trực của đoạn thẳng BC cắt BC tại I, cắt AC tại H, cắt AB tại D. Chứng minh rằng:
a. Tam giác DBC là tam giác cân
b. BH vuông góc với DC
c. AH<HC
Mong mọi người giúp nhé, mình đang cần gấp
Bài 3: Cho tam giác ABC= tam giác DEF.Viết tên cạnh và các góc = nhau.Vẽ hình
GIÚP MK NHA MAI MK HỌC RÙI MK CẦN GẤP LẮM
Cho ABC có ΔAB=9cm; AC=12cm. Kẻ đường trung tuyến AM, G là trọng tâm của ΔABC. Trên tia đối của tia MA lấy điểm D sao cho MD=MA.
a)Tính AM,AG.
b)Chứng minh: AB=CD.
c)Chứng minh: Góc BAM> góc MAC.
d)Lấy I thuộc BC sao cho IC=5cm; tia DI cắt AC tại K.
e)Chứng minh: ΔKGI là tam giác cân.
GIÚP MÌNH VỚI MÌNH CẦN GẤP Ạ. CẢM ƠN MỌI NGƯỜI Ạ!
Tam giác ABC cân tại A. Kẻ BD vuông góc AC, CE vuông góc AB (D thuộc AC, E thuộc AB).
a/ Chứng minh DB = CE
b/ Gọi H là giao điểm của DB và CE. Chứng minh tam giác HCB cân
c/ Chứng minh AH là tia phân giác của góc BAC
d/ Đường thẳng vuông góc với BD tại B và đường thẳng vuông góc với CE tại C cắt nhau tại M. Chứng minh 3 điểm A, H, M thẳng hàng
P/s: mọi người giúp dùm mình với ạ, ngày mai mình phải thi rồi T.T Cảm ơn mọi người nhiều lắm ạ ^^