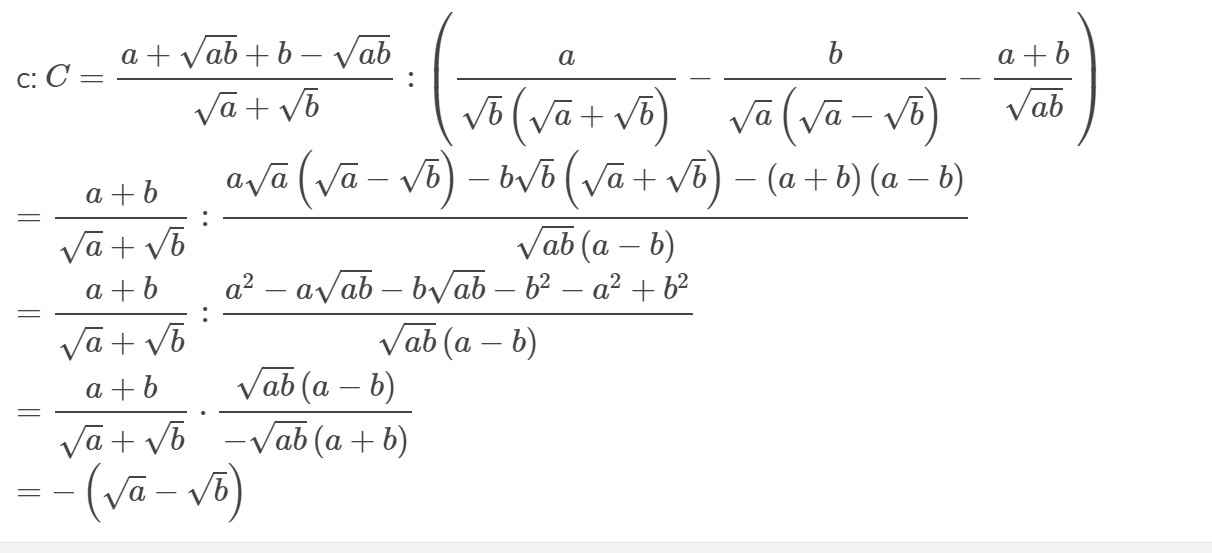Ôn thi vào 10
Các câu hỏi tương tự
3.P=\(\left(\dfrac{3\sqrt{a}}{a+\sqrt{ab}+b}-\dfrac{3a}{a\sqrt{a}-b\sqrt{b}}+\dfrac{1}{\sqrt{a}-\sqrt{b}}\right)\):\(\left(\dfrac{\left(a-1\right).\left(\sqrt{a}-\sqrt{b}\right)}{2a+2\sqrt{ab}+2b}\right)\)
a)Rút gọn P
b)Tìm những giá trị nguyên của a để P có giá trị nguyên
Câu 1.Cho hai biểu thức Adfrac{sqrt{x}+2}{1+sqrt{x}} và Bleft(dfrac{2sqrt{x}}{x-sqrt{x}-6}+dfrac{sqrt{x}}{sqrt{x}-3}right):dfrac{sqrt{x}}{sqrt{x}-3} với xge0,xne9.1) Tính giá trị biểu thức A khi x 36.2) Rút gọn biểu thức B.3) Với x ∈ mathbb{Z}, tìm giá trị lớn nhất của biểu thức P A.B.Câu 2.Giải bài toán sau bằng cách lập hệ phương trình:Theo kế hoạch, hai xí nghiệp A và B phải làm tổng cộng 720 dụng cụ cùng loại. Trên thực tế do cải tiến kĩ thuật, xí nghiệp A hoàn thành vượt mức 12%, còn xí n...
Đọc tiếp
Câu 1.
Cho hai biểu thức \(A=\dfrac{\sqrt{x}+2}{1+\sqrt{x}}\) và \(B=\left(\dfrac{2\sqrt{x}}{x-\sqrt{x}-6}+\dfrac{\sqrt{x}}{\sqrt{x}-3}\right):\dfrac{\sqrt{x}}{\sqrt{x}-3}\) với \(x\ge0,x\ne9\).
1) Tính giá trị biểu thức A khi x = 36.
2) Rút gọn biểu thức B.
3) Với x ∈ \(\mathbb{Z}\), tìm giá trị lớn nhất của biểu thức P = A.B.
Câu 2.
Giải bài toán sau bằng cách lập hệ phương trình:
Theo kế hoạch, hai xí nghiệp A và B phải làm tổng cộng 720 dụng cụ cùng loại. Trên thực tế do cải tiến kĩ thuật, xí nghiệp A hoàn thành vượt mức 12%, còn xí nghiệp B hoàn thành vượt mức 10% so với kế hoạch. Do đó thực tế cả hai xí nghiệp làm được tổng cộng 800 dụng cụ. Tính số dụng cụ mỗi xí nghiệp phải làm theo kế hoạch?
Câu 3.
1) Giải phương trình: 3x4 - 2x2 - 40 = 0
2) Cho phương trình x2 + (m - 1)x - m2 - 2 = 0 (1), với m là tham số thực.
a) Chứng minh phương trình (1) luôn có hai nghiệm trái dấu x1, x2 với mọi giá trị của m.
b) Tìm m để biểu thức \(T=\left(\dfrac{x_1}{x_2}\right)^3+\left(\dfrac{x_2}{x_1}\right)^3\) đạt giá trị lớn nhất.
Câu 4.
Cho (O; R) và một điểm P nằm ngoài đường tròn. Kẻ hai tiếp tuyến PA, PB với đường tròn (A, B là tiếp điểm). Tia PO cắt đường tròn tại hai điểm K và I (K nằm giữa P và O) và cắt AB tại H. Gọi D là điểm đối xứng với B qua O, C là giao điểm của PD với đường tròn (O).
1) Chứng minh tứ giác BHCP nội tiếp.
2) Chứng minh PC.PD = PO.PH.
3) Đường tròn ngoại tiếp tam giác ACH cắt IC tại M. Tia AM cắt BI tại Q. Chứng minh tam giác AQH cân.
4) Giả sử \(\widehat{BDC}=45^o\). Tính diện tích tam giác PBD phần nằm bên ngoài đường tròn (O) theo R.
Câu 5.
Tìm m để phương trình ẩn x sau đây có ba nghiệm phân biệt. x3 - 2mx2 + (m2 + 1)x - m = 0.
c1
cho biểu thức
\(A=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}+\dfrac{2+5\sqrt{x}}{4-x}\)vs \(x\ge0,x\ne4\)
a/ rút gọn A
b/ tìm x để A=2
6 tháng 12 2023 lúc 5:12
Cho biểu thức B = \(\left(\dfrac{x-y}{\sqrt{x}-\sqrt{y}}+\dfrac{x\sqrt{x}-y\sqrt{y}}{y-x}\right):\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+\sqrt{xy}}{\sqrt{x}+\sqrt{y}}\)
a) Rút gọn biểu thức B
b) Chứng minh \(B\ge0\)
Câu I.Cho hai biểu thức Adfrac{2sqrt{x}+1}{x^2} và Bleft(dfrac{4x}{sqrt{x}-1}-dfrac{sqrt{x}-2}{x-3sqrt{x}+2}right)timesdfrac{sqrt{x}-1}{x^2} với xge0,xne4.1) Tính giá trị của A tại x 9.2) Rút gọn B.3) Tìm x để B A.Câu II.1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:Hai đội công nhân A và B cùng nhau làm một công việc thì hoàn thành trong 16 ngày. Nếu đội A làm trong 4 ngày rồi nghỉ, và tiếp theo đội B làm 3 ngày thì cả hai hoàn thành được dfrac{11}{48} công việc. Hỏi nế...
Đọc tiếp
Câu I.
Cho hai biểu thức \(A=\dfrac{2\sqrt{x}+1}{x^2}\) và \(B=\left(\dfrac{4x}{\sqrt{x}-1}-\dfrac{\sqrt{x}-2}{x-3\sqrt{x}+2}\right)\times\dfrac{\sqrt{x}-1}{x^2}\) với \(x\ge0,x\ne4.\)
1) Tính giá trị của A tại x = 9.
2) Rút gọn B.
3) Tìm x để B < A.
Câu II.
1) Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Hai đội công nhân A và B cùng nhau làm một công việc thì hoàn thành trong 16 ngày. Nếu đội A làm trong 4 ngày rồi nghỉ, và tiếp theo đội B làm 3 ngày thì cả hai hoàn thành được \(\dfrac{11}{48}\) công việc. Hỏi nếu mỗi đội làm riêng thì làm xong công việc đó trong mấy ngày?
2) Một hình trụ có chiều cao bằng 2 lần bán kính đáy. Tính diện tích toàn phần của hình trụ đó biết thể tích của hình trụ là 128π (cm3).
Câu III.
1) Giải hệ phương trình: \(\left\{{}\begin{matrix}x-2y+\dfrac{1}{2x+3y}=2\\2x-4y+\dfrac{3}{2x+3y}=3\end{matrix}\right.\)
2) Cho phương trình \(x^2-\left(m-3\right)x+2m-11=0\) ( với m là tham số)
a) Chứng minh rằng phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m.
b) Tìm m để phương trình có hai nghiệm phân biệt x1, x2 là độ dài hai cạnh của một tam giác vuông với cạnh huyền bằng 4.
Câu IV.
Cho tam giác nhọn ABC nội tiếp đường tròn tâm (O) và AC > BC. Gọi AD, BE, CF là ba đường cao, H là trực tâm của tam giác ABC. Gọi M, N lần lượt là trung điểm của AD, AC. Tia CO cắt DE tại P.
1) Chứng minh rằng tứ giác ABDE nội tiếp và △ABD đồng dạng với △CON.
2) Chứng minh rằng CP⊥DE và \(\widehat{FCP}=\widehat{ABC}-\widehat{CAB}.\)
3) Chứng minh rằng \(\widehat{MNF}=\widehat{FCP}\) và tứ giác FMPD nội tiếp.
Câu V.
Giải phương trình: \(\left(\sqrt{x+1}-\sqrt{x-2}\right).\left(\sqrt{4-x}+1\right)=2\).
Rút gọn bthuc ( ko dùng mt cầm tay)
\(\dfrac{a+b-2\sqrt{ab}}{\left(\sqrt{a}-\sqrt{b}\right)}\):\(\dfrac{1}{\sqrt{a}+\sqrt{b}}\) ( a>0, b>0, a khác b).
29 tháng 10 2021 lúc 21:37
\(A=\dfrac{-3\sqrt{x}+1}{\sqrt{x}-3}\) và \(B=\dfrac{3\sqrt{x}-2}{x-5\sqrt{x}+6}-\dfrac{1}{\sqrt{x}-2}+\dfrac{3\sqrt{x}-2}{3-\sqrt{x}}\) \(\left(x\ge0;x\ne4;x\ne9\right)\). Với \(x>9\), so sánh \(\dfrac{A}{B}\) và 1.
Bài 1: Rút gọn các biểu thức sau:a) (left(sqrt{12}-sqrt{75}+sqrt{48}right):sqrt{3}b) dfrac{sqrt{8-4sqrt{3}}}{sqrt{3-1}}c) left(dfrac{1-asqrt{a}}{1-sqrt{a}}+sqrt{a}right)left(dfrac{1-sqrt{a}}{1-a}right) với 0 le a ne1Bài 2: a) Vẽ đồ thị (P) của hàm số y ax2b) Chứng minh rằng đường thẳng (d) y kx +1 luôn cắt đồ thị (P) tại hai điểm phân biệt với mọi kBài 3a) Giải hệ phương trình: left{{}begin{matrix}2x-2y-2dfrac{1}{2}x+dfrac{2}{3}y5end{matrix}right.b) Giải phương trình: x4 +x2 -2 0c) Cho phương...
Đọc tiếp
Bài 1: Rút gọn các biểu thức sau:
a) (\(\left(\sqrt{12}-\sqrt{75}+\sqrt{48}\right):\sqrt{3}\)
b) \(\dfrac{\sqrt{8-4\sqrt{3}}}{\sqrt{3-1}}\)
c) \(\left(\dfrac{1-a\sqrt{a}}{1-\sqrt{a}}+\sqrt{a}\right)\left(\dfrac{1-\sqrt{a}}{1-a}\right)\) với 0 \(\le\) a \(\ne\)1
Bài 2:
a) Vẽ đồ thị (P) của hàm số y = ax2
b) Chứng minh rằng đường thẳng (d) y = kx +1 luôn cắt đồ thị (P) tại hai điểm phân biệt với mọi k
Bài 3
a) Giải hệ phương trình: \(\left\{{}\begin{matrix}2x-2y=-2\\\dfrac{1}{2}x+\dfrac{2}{3}y=5\end{matrix}\right.\)
b) Giải phương trình: x4 +x2 -2 = 0
c) Cho phương trình: x2 - 2(m-1)x + 2m -4 =0 có hai nghiệm x1x2. Tìm giá trị nhỏ nhất của biểu thức A = x11x22
Bài 4: Hai người cùng làm chung một công việc trong \(\dfrac{12}{5}\) giờ thì xong. Nếu mỗi người làm một mình thì người thứ nhất hoàn thành công việc trong ít hơn người thứ hai là 2 giờ. Hỏi nếu làm một mình thì mỗi người phải làm trong bao nhiêu thời gian để xong công việc?
Bài 5: Cho đường tròn(O;R) từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d) lấy điểm M bất kì ( M khác A) kẻ các tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC vuông góc MB, BD vuông góc MA, gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB
a) Chứng minh tứ giác AMBO nội tiếp
b) Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn
c) Chứng minh OI.OM = R2; OI. IM = IA2
d) Chứng ming OAHB là hình thoi
e) Chứng minh ba điểm O,H,M thẳng hàng
23 tháng 9 2023 lúc 19:57
Cho biểu thức:
P = \(\left(\dfrac{4\sqrt{x}}{2+\sqrt{x}}+\dfrac{8x}{4-x}\right):\left(\dfrac{\sqrt{x}-1}{x-2\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\left(x>0,x\ne4,x\ne9\right)\)
a) Rút gọn P
b) Với \(x>9\), tìm GTNN của P