BT1: dựa vào tính chất của hình chữ nhật, chứng tỏ rằng : trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy và ngược lại
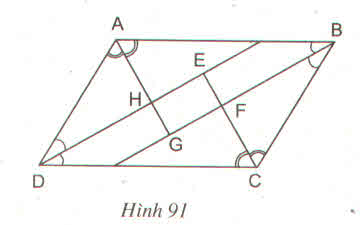
BT2: cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 72. chứng minh rằng EFGH là hình chữ nhật
BT3: cho hình bình hành ABCD. Gọi E, F tương ứng là trung điểm của CD và AB
a) chứng minh rằng AECF là một hình bình hành
b) AE cắt BD tại I , còn CF cắt BD tại H. chứng minh rằng DI = IH = HB
c) gọi J là giao điểm của BE với CF. chứng minh rằng 4HJ = HC
Bài 3:
a: Xét tứ giác AECF có
AF//CE
AF=CE
Do đó: AECF là hình bình hành
b: Xét ΔAIB có
F là trung điểm của AB
FH//AI
Do đó: H là trung điểm của BI
=>BH=HI(1)
Xét ΔDHC có
E là trung điểm của DC
EI//HC
Do đó: I là trung điểm của DH
=>DI=IH(2)
Từ (1) và (2) suy ra DI=IH=HB