Bài giải: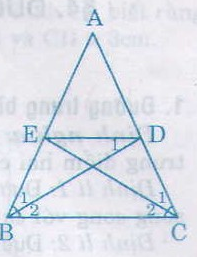 
a) ∆ABD và ∆ACE có
AB = AC (gt)
\(\widehat{A}\) chung
\(\widehat{B_1}=\widehat{C_1}\left(=\dfrac{1}{2}\widehat{B}=\dfrac{1}{2}\widehat{C}\right)\)
Nên ∆ABD = ∆ACE (g.c.g)
Suy ra AD = AE
Chứng minh BEDC là hình thang cân như câu a của bài 15.
b) Vì BEDC là hình thang cân nên DE // BC.
Suy ra \(\widehat{D_1}=\widehat{B_2}\) (so le trong)
Lại có \(\widehat{B_2}=\widehat{B_1}\) nên \(\widehat{B_1}=\widehat{D_1}\)
Do đó tam giác EBD cân. Suy ra EB = ED.
Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.
Chúc bạn học tốt!
Đúng 0
Bình luận (1)
Giúp mình vs
Bài 26 (SBT Toán 8-tr.83)