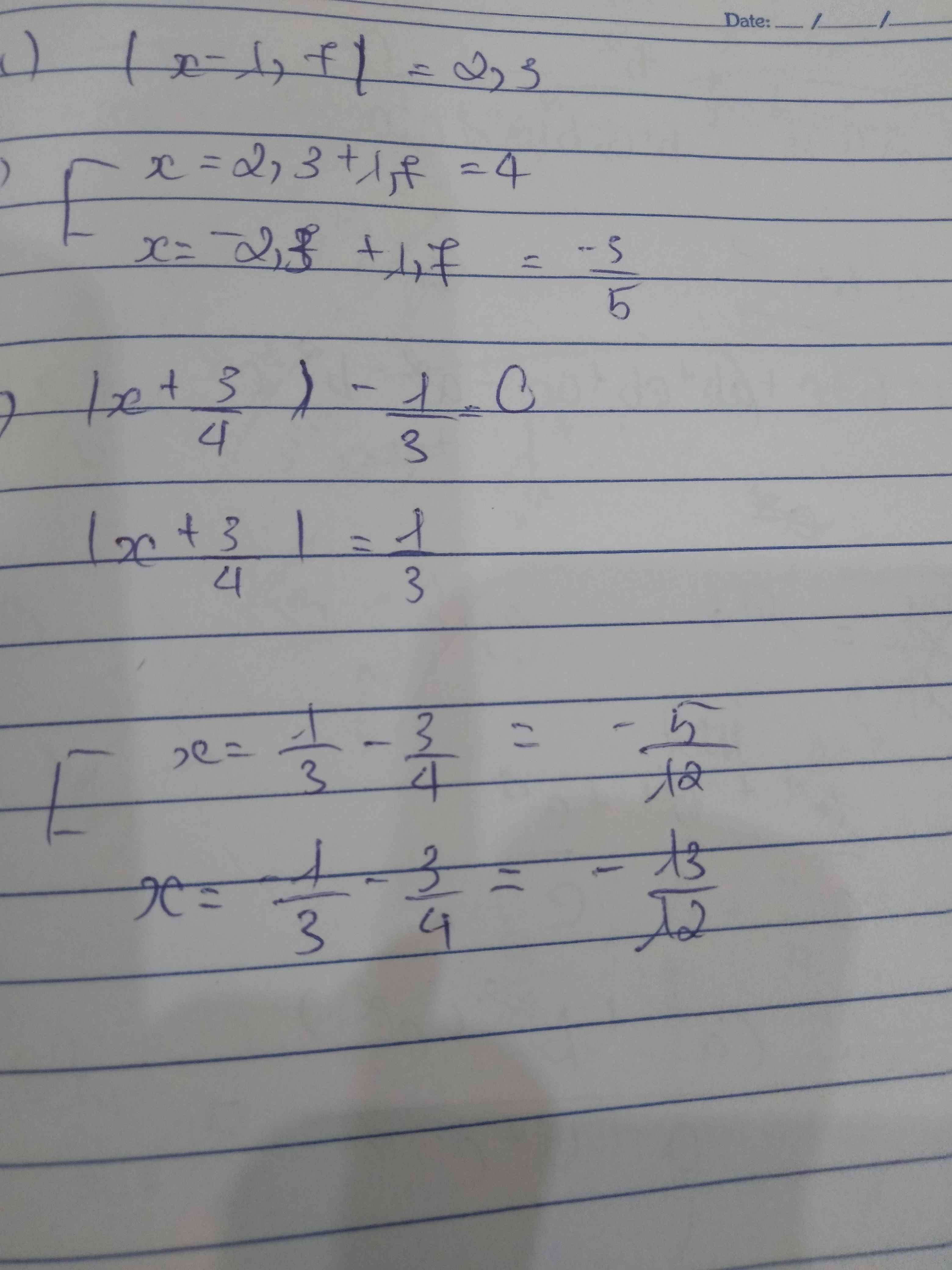a, Ta có
\(\left|x-1,7\right|=2,3\\ \Rightarrow\left[{}\begin{matrix}x-1,7=2.3\\x-1.7=-2,3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=4\\x=-0,6\end{matrix}\right.\)
Vậy....
b, Ta có :
\(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{3}=0\\ \Rightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{3}\\ \Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=-\dfrac{5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
Vậy...
a) \(\left|x-1,7\right|=2,3\)
\(\Rightarrow\left[{}\begin{matrix}x-1,7=2,3\\x-1,7=\left(-2,3\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2,3+1,7\\x=\left(-2,3\right)+1,7\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=\left(-0,6\right)\end{matrix}\right.\)
Vậy x=4 hoặc x = (-0,6)
b) \(\left|x+\dfrac{3}{4}\right|-\dfrac{1}{3}=0\)
\(\Rightarrow\left|x+\dfrac{3}{4}\right|=0+\dfrac{1}{3}\)
\(\Rightarrow\left|x+\dfrac{3}{4}\right|=\dfrac{1}{3}\)
\(\Rightarrow\left[{}\begin{matrix}x+\dfrac{3}{4}=\dfrac{1}{3}\\x+\dfrac{3}{4}=-\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}-\dfrac{3}{4}\\x=-\dfrac{1}{3}-\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{12}-\dfrac{9}{12}\\x=-\dfrac{4}{12}-\dfrac{9}{12}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{-5}{12}\\x=-\dfrac{13}{12}\end{matrix}\right.\)
Vậy \(x=\dfrac{-13}{12}\) hoặc \(x=\dfrac{-5}{12}\)