Bài 3. Cho góc đỉnh O khác góc bẹt a) Từ một điểm M trên tia phân giác của góc O, kẻ các đường vuông góc MA, MB đến hai cạnh của góc này. Chứng minh rằng AB⊥OM
b) Trên hai cạnh của góc O lấy hai điểm C và D, sao cho OC = OD. Hai đường thẳng lần lượt vuông góc với hai cạnh của góc O tại C và D cắt nhau ở E. Chứng minh rằng OE là tia phân giác của góc O.
Bài 4. Cho tam giác cân ABC, AB = AC. Trên các cạnh AB, AC lần lượt lấy hai điểm P, Q sao cho AP = AQ. Hai đoạn thẳng CP, BQ cắt nhau tại O. Chứng minh rằng:
a) Tam giác OBC là tam giác cân.
b) Điểm O cách đều hai cạnh AB, AC.

a,Gọi I là giao điểm của OM và AB
Xét ∆AOM vuông tại A và ∆BOM vuông tại B có
OM : cạnh chung
AOM = BOM (OM là phân giác của góc O và A , B thuộc 2 canhn của góc này)
=>∆AOM = ∆BOM (cạnh huyền - góc nhọn)
=> MA = MB (2 cạnh tương ứng)
và AMO = BMO (2 góc tương ứng)
Xét ∆AMI và ∆BMI có
MI : chung
AMO = BMO (cmt)
MA = MB (cmt)
=>∆AMI = ∆BMI (c.g.c)
=> AIM = BIM (2 góc tương ứng)
Mà 2 góc này kề bù
=> AIM = BIM = 90°
Lại có AB cắt OM tại I
=> AB vuông góc vs OM tại I
b, Xét ∆COE vuông tại C và ∆DOE vuông tại D có
OE : chung
OC = OD (gt)
=>∆COE = ∆DOE (cạnh huyền.cạnh góc vuông)
=> COE = DOE (2 góc tương ứng)
=> OE là phân giác góc O
Bài 4:
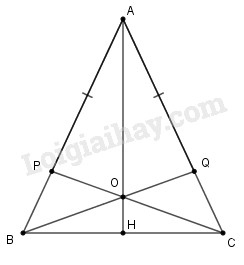
a) Vì \(\Delta ABC\) cân có \(AB=AC\left(gt\right)\)
=> \(\Delta ABC\) cân tại \(A.\)
=> \(\widehat{ABC}=\widehat{ACB}\) (tính chất tam giác cân).
Xét 2 \(\Delta\) \(ABQ\) và \(ACP\) có:
\(AB=AC\left(gt\right)\)
\(\widehat{A}\) chung
\(AQ=AP\left(gt\right)\)
=> \(\Delta ABQ=\Delta ACP\left(c-g-c\right).\)
=> \(\widehat{ABQ}=\widehat{ACP}\) (2 góc tương ứng).
+ Ta có:
\(\left\{{}\begin{matrix}\widehat{ABQ}+\widehat{QBC}=\widehat{ABC}\\\widehat{ACP}+\widehat{PCB}=\widehat{ACB}\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}\widehat{ABQ}=\widehat{ACP}\left(cmt\right)\\\widehat{ABC}=\widehat{ACB}\left(cmt\right)\end{matrix}\right.\)
=> \(\widehat{QBC}=\widehat{PCB}.\)
Hay \(\widehat{OBC}=\widehat{OCB}.\)
=> \(\Delta OBC\) cân tại \(O.\)
b) Vì \(\Delta OBC\) cân tại \(O\left(cmt\right).\)
=> \(OB=OC\) (tính chất tam giác cân).
Xét 2 \(\Delta\) \(AOB\) và \(AOC\) có:
\(AB=AC\left(gt\right)\)
\(OB=OC\left(cmt\right)\)
Cạnh AO chung
=> \(\Delta AOB=\Delta AOC\left(c-c-c\right).\)
=> \(\widehat{BAO}=\widehat{CAO}\) (2 góc tương ứng).
=> \(AO\) là tia phân giác của \(\widehat{BAC}.\)
=> \(O\) cách đều hai cạnh \(AB,AC\) (Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó) (đpcm).
Chúc bạn học tốt!












