Bài 5: Tính chất đường phân giác của một góc
Nội dung lý thuyết
1. Định lí về tính chất các điểm thuộc tia phân giác
Định lí 1 (định lí thuận):
Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Cụ thể: Một điểm \(M\) bất kì nằm trên tia phân giác của góc \(xOy\). Kẻ \(MH\perp Ox,MK\perp Oy\) thì ta có khoảng cách từ \(M\) đến \(Ox\) bằng \(MH\) và khoảng cách từ \(M\) đến \(Oy\) bằng \(MK\) . Khi đó \(MH=MK\):

Chứng minh:
Xét \(\Delta OMH\) và \(\Delta OMK\) vuông có:
Cạnh huyền \(OM\) chung ;
\(\widehat{HOM}=\widehat{KOM}\) (do \(M\) nằm trên tia phân giác của góc \(xOy\))
Nên \(\Delta OMH=\Delta OMK\) (cạnh huyền - góc nhọn)
Từ đó ta suy ra \(MH=MK\) (hai cạnh tương ứng)
Ví dụ: Điểm \(A\) nằm trên tia phân giác \(Ot\) của góc \(\widehat{mOn}\). Biết khoảng cách từ \(A\) đến tia \(Om\) là \(3,5cm\). Tính khoảng cách từ \(A\) đến \(On\).
Giải:
Do \(A\) nằm trên tia phân giác của góc \(\widehat{mOn}\)
Nên \(d\left(A;Om\right)=d\left(A;On\right)\)
Mà \(d\left(A;Om\right)=3,5cm\)
Suy ra \(d\left(A;On\right)=3,5cm\)
@1712349@
2. Định lí đảo
Xét bài toán: Cho một điểm \(M\) nằm trong góc \(xOy\) sao cho khoảng cách từ \(M\) đến hai cạnh \(Ox\), \(Oy\) bằng nhau. Hỏi điểm \(M\) có nằm trên tia phân giác của góc \(xOy\) không?
Giải:
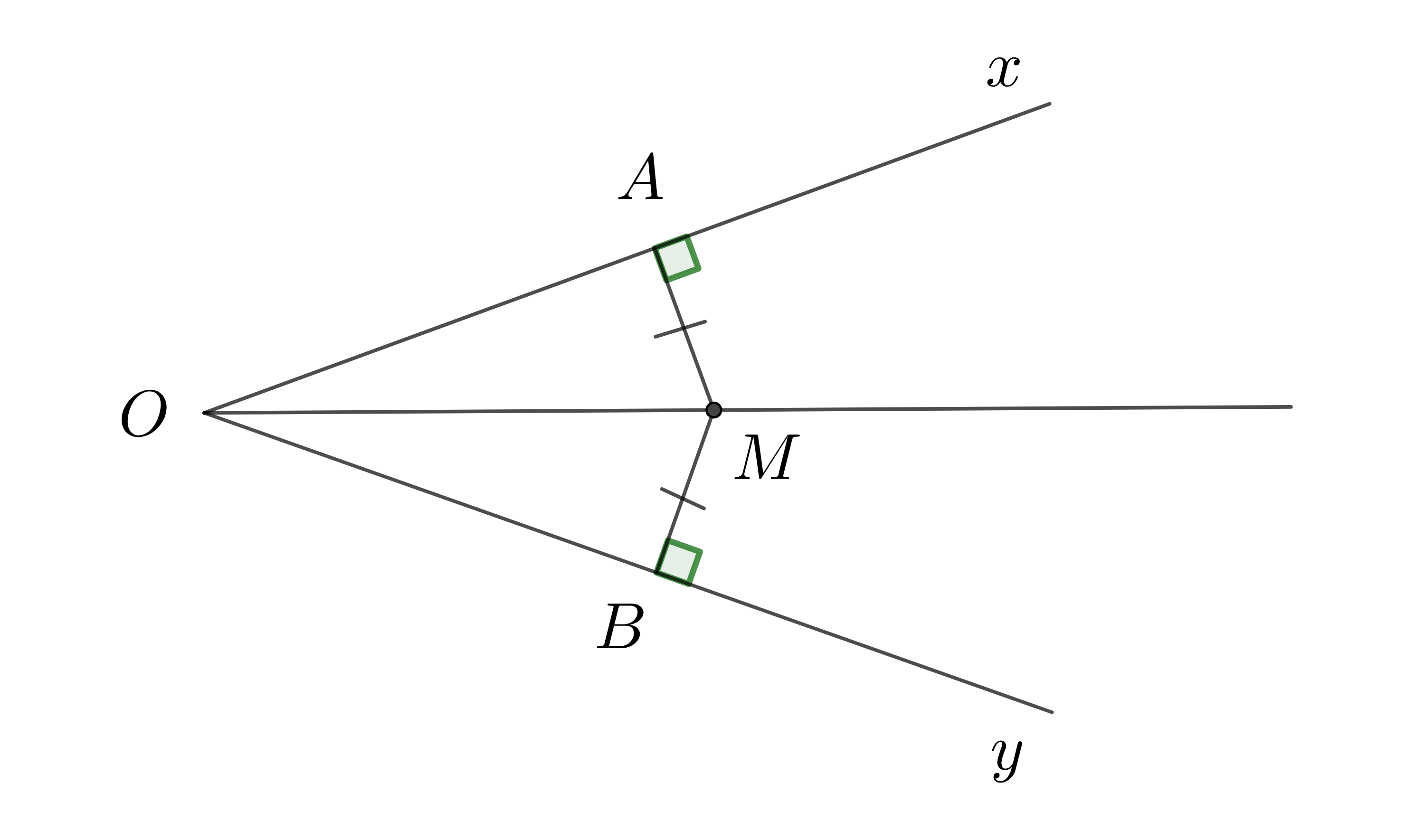
Kẻ tia \(OM\).
Kẻ \(MA\perp Ox,MB\perp Oy\). Theo đề bài ta có \(MA=MB\)
Xét \(\Delta OAM\) và \(\Delta OBM\) có:
Cạnh huyền \(OM\) chung ;
\(MA=MB\) (gt)
\(\Rightarrow\Delta OAM=\Delta OBM\) (cạnh huyền - cạnh góc vuông)
Suy ra \(\widehat{AOM}=\widehat{BOM}\) (hai góc tương ứng)
Do đó \(OM\) là tia phân giác của góc \(xOy\) hay \(M\) nằm trong tia phân giác của góc \(xOy\).
Định lí 2 (Định lí đảo):
Điểm nằm bên trong một góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
Nhận xét:
Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó.
Ví dụ: Cho tam giác \(ABC\) có \(BD,CE\) lần lượt là tia phân giác của góc \(B\) và góc \(C\). Biết rằng \(BD,CE\) cắt nhau tại \(I\). Chứng minh rằng \(I\) cách đều \(AB\) và \(AC\).
Giải:

Do \(I\in BD\) là tia phân giác góc \(B\) nên \(d\left(I,AB\right)=d\left(I,BC\right)\)
Do \(I\in CE\) là tia phân giác góc \(C\) nên \(d\left(I,AC\right)=d\left(I,BC\right)\)
Suy ra \(d\left(I,AB\right)=d\left(I,AC\right)\)
@1726129@