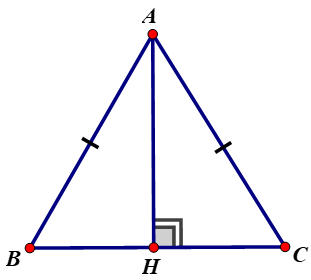
Bài 1:Cho tam giác cân ABC có AB=AC =5 cm, BC=8cm.Kẻ AH vuông góc với BC (H thuộc BC)
a)Chứng minh:HB=HC và CAH=BAH
b)Tính độ dài AH ?
Bài 2:Cho tam giác DEF vuông tại D, phân giác EB.Kẻ BI vuông góc với EF tại I.Gọi H là giao điểm của ED và IB.Chứng minh:
a)Tam giác EDB= tam giác EIB
b)HB=BF
Giúp mình nhé, đầu năm mình ko muốn bị phạt đâu :(
Bài 1:
=> \(\widehat{BAH}=\widehat{CAH}\) (2 góc tương ứng).
Vậy \(AH=3\left(cm\right).\)
Chúc bạn học tốt!
Bài 1:
a) Xét ΔABH vuông tại H và ΔAHC vuông tại H có
AB=AC(do ΔABC cân tại A)
AH là cạnh chung
Do đó: ΔABH=ΔAHC(cạnh huyền-cạnh góc vuông)
⇒BH=CH(hai cạnh tương ứng)
Ta có: ΔABH=ΔAHC(cmt)
⇒\(\widehat{BAH}=\widehat{CAH}\)(hai góc tương ứng)
b) Ta có: HB=HC(cmt)
mà H∈BC(gt)
nên H là trung điểm của BC
⇒\(HB=HC=\frac{BC}{2}=\frac{8}{2}=4cm\)
Áp dụng định lí pytago vào ΔABH vuông tại H, ta được
\(AB^2=AH^2+BH^2\)
hay \(AH^2=AB^2-BH^2=5^2-4^2=9\)
⇒\(AH=\sqrt{9}=3cm\)
Vậy: AH=3cm
Bài 2:
a) Xét ΔEDB vuông tại D và ΔEIB vuông tại I có
EB là cạnh chung
\(\widehat{DEB}=\widehat{IEB}\)(do EB là tia phân giác của \(\widehat{DEI}\))
Do đó: ΔEDB=ΔEIB(cạnh huyền-góc nhọn)
b)Ta có: ΔEDB=ΔEIB(cmt)
⇒DB=IB(hai cạnh tương ứng)
Xét ΔDBH vuông tại D và ΔIBF vuông tại I có
DB=IB(cmt)
\(\widehat{DBH}=\widehat{IBF}\)(hai góc đối đỉnh)
Do đó: ΔDBH=ΔIBF(cạnh góc vuông-góc nhọn kề)
⇒HB=BF(hai cạnh tương ứng)