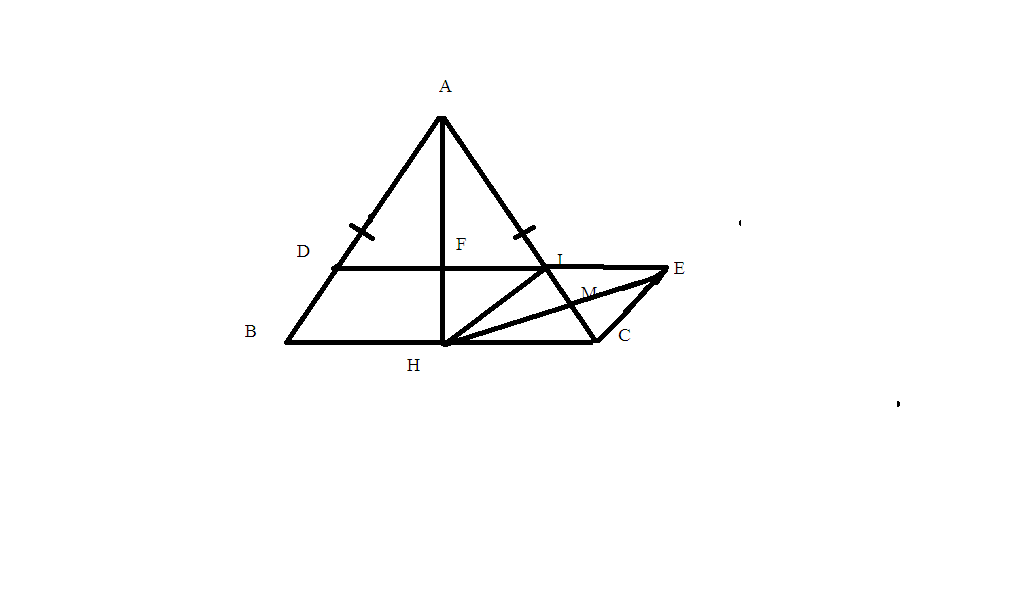
bài 1: cho tam giác ABC cân tại A, H là trung điểm của BC.
a) CM AH vuông góc BC
B)Lấy D thuộc AB, I thuộc AC sao cho BD=CI. CM HA là tia phân giác của góc DHI
c) Gọi M là trung điểm của IC, qua C kẻ đường thẳng song song với HI cắt MH tại E. CM EI//HC và D,I,E thẳng hàng.
Bài 2:
Cho tam giác ABC, kẻ BM vuông góc AC tại M, biết BM=8cm; AB=10cm; MC=15cm. Tính BC,AM. Hỏi tam giác ABC có vuông không? Tại sao?
a) Xét ΔABH và ΔACH có:
AB=AC (ΔABC cân tại A)
AH là cạnh chung
HB=HC(H là trung điểm của BC)
Nên ΔABH =ΔACH (c.c.c)
=>\(\widehat{AHB}=\widehat{AHC}\)( 2 GÓC TƯƠNG ỨNG)
Ta có: \(\widehat{AHB}+\widehat{AHC}=180^O\)( 2 góc kề bù)
=>\(\widehat{AHB}.2=180^O\Rightarrow\widehat{AHB}=90^O\)
=>AH ⊥ BC
b) Vì ΔABH =ΔACH => \(\widehat{BAH}=\widehat{CAH}\)
Ta có: AD+BD=AB ( D nằm giữa A và B)
AI+IC=AC( I nằm giữa A và C)
Mà AB=AC, BD=IC =>AD=AI
Cho AH và DI cắt nhau tại F
Xét ΔDFA và ΔIFA có:
FA là cạnh chung
\(\widehat{BAH}=\widehat{CAH}\)
AD=AI
Nên ΔDFA=ΔIFA (c.g.c)
=>\(\widehat{DAF}=\widehat{IAF}\)
=>A là tia phân giác của góc DHI













