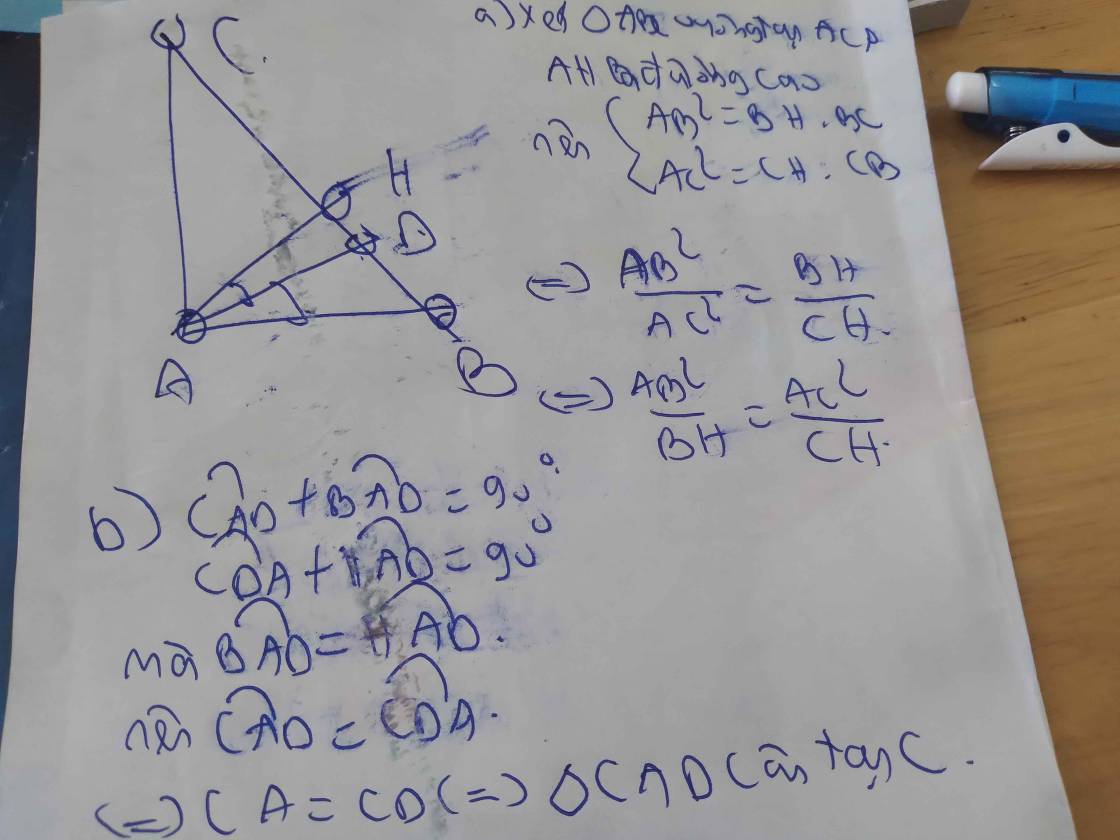Ôn tập Hệ thức lượng trong tam giác vuông
Các câu hỏi tương tự
Cho tam giác ABC vuông tại A( AB>AC), đường cao AH. Gọi M là trung điểm của AB,AD là phân giác của góc BAH (D thuộc BH),MD cắt AH tại E.
a)Chứng minh rằng: \(\dfrac{AB^2}{BH}=\dfrac{AC^2}{CH}\)
b)Tính độ dài AH biết diện tích các tam giác AHC và ABH lần lượt là 8,64 cm2 và 15,36cm2 .
c) Chứng minh rằng: CE//AD
Cho tam giác ABC vuông tại A, đường phân giác AD. Chứng minh rằng √2/AD = 1/AB + 1/AC. Kẻ đường cao AH và đường trung tuyến AM của tam giác ABC chứng minh rằng nếu 1/ah^2+1/am^2=2/ad^2. Giúp mình câu 2 thôi ạ mình cảm ơn
Cho tam giác ABC vuông tại A có AB=9cm AC=12cm BC=15cm. Kẻ đường cao AH và trung tuyến AO. Tia phân giác trong và ngoài của góc BAC lần lượt cắt BC tại D, E. Chứng minh \(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{\sqrt{2}}{AD}\)
Cho tam giác ABC biết AB=AC=15cm, BC=24cm và đường cao AH
a. Tính các góc của tam giác ABC
b. Lấy M trên HC, từ ME kẻ vuông góc AB và MF vuông góc AC. Tính tổng ME+MF
c. Vẽ đường cao BK của tam giác ABC. CM: góc BAK= 2 góc HKA
làm câu c giúp mình thôi ạ
Cho tam giác nhọn ABC, đường cao AD (D thuộc BC). Gọi M, N lần lượt là hình chiếu vuông góc của D trên AB, AC. Chứng minh rằng:
1. Hai tam giác AMN và ACB đồng dạng.
2. MN=AD.sin BAC
Giúp mình câu 2 với ạ, mình đang cần gấp. Mình cảm ơn ạ
Cho tam giác ABC vuông tại A, đường cao AH.a.Cho sinABCdfrac{3}{5}, BC20cm. Tính các cạnh AB, AC, BH và góc ACBb) Đường thẳng vuông góc với BC tại B cắt đường thẳng AC tại D. Chứng minh: AD.AC BH.BC
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH.
a.Cho sinABC=\(\dfrac{3}{5}\), BC=20cm. Tính các cạnh AB, AC, BH và góc ACB
b) Đường thẳng vuông góc với BC tại B cắt đường thẳng AC tại D.
Chứng minh: AD.AC = BH.BC
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC
a, Cho AB=9, BH=5.4. Tính AC,BC,AH,EF ( đã làm được)
b, Chứng minh \(\dfrac{1}{EF^2}\)=\(\dfrac{1}{AB^2}\)+\(\dfrac{1}{AC^2}\)(đã làm được)
c, Chứng minh EA.EB+FA.FC=HB.HC( cần trợ giúp)
cho ΔABC vuông tại A, đường cao AH.Gọi E,F lần lượt là hình chiếu của H trên AB,AC.1)Cho AB9cm,BH5,4cm.Tính các cạnh AC,BC,AH,FE.Tính các góc ABC,HAC(làm tròn đến độ)2) Tính diện tích tứ giác AEHF, tam giác AFE3) Kẻ đường phân giác AD,từ D kẻ DPperpAB,DQperpAC.Tính BD,CD,AD, chu vi và diện tích AQDP4) chứng minh rằng:a) AE.ABAF.ACHB.HC b)BCAB.cosB+AC.cosCc)tanB.sinBHC/AB d)cosC.sinBHC/BC5)Chứng minh rằng: 1/EF2 1/AB2 + 1/AC2 6) Chứng minh rằng: EA.EB+FA.FCHB.HC
Đọc tiếp
cho ΔABC vuông tại A, đường cao AH.Gọi E,F lần lượt là hình chiếu của H trên AB,AC.
1)Cho AB=9cm,BH=5,4cm.Tính các cạnh AC,BC,AH,FE.Tính các góc ABC,HAC(làm tròn đến độ)
2) Tính diện tích tứ giác AEHF, tam giác AFE
3) Kẻ đường phân giác AD,từ D kẻ DP\(\perp\)AB,DQ\(\perp\)AC.Tính BD,CD,AD, chu vi và diện tích AQDP
4) chứng minh rằng:
a) AE.AB=AF.AC=HB.HC b)BC=AB.cosB+AC.cosC
c)tanB.sinB=HC/AB d)cosC.sinB=HC/BC
5)Chứng minh rằng: 1/EF2 =1/AB2 + 1/AC2
6) Chứng minh rằng: EA.EB+FA.FC=HB.HC
Cho tam giác vuông ABC vuông tại a AB bé hơn AC có đường cao AH (H thuộc BC) AB = 3 BH =1,8 A) tính BC AH AC B) kẻ HD vuông AC (D thuộc AC) chứng minh HC = AD.AC/HB C) gọi e là điểm đối xứng với H qua AB. Chứng minh S tam giác AED = sin²AHD . S tam giác ACE