a) Xét hàm số y = -x3 + 3x + 1. Tập xác định : R.
y' = -3x2 + 3 = -3(x2 - 1); y' = 0 ⇔ x = -1,x = 1.
Bảng biến thiên:
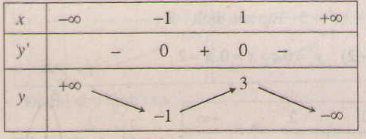
Đồ thị (C) như hình bên.

b) x3 - 3x + m = 0 ⇔ -x3 + 3x + 1 = m + 1 (1). Số nghiệm của (1) chính là số giao điểm của đồ thị (C) với đường thẳng (d) : y = m + 1.
Từ đồ thị ta thấy :
m + 1 < -1 ⇔ m < -2 : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.
m + 1 = -1 ⇔ m = -2 : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.
-1 < m + 1 < 3 ⇔ -2 < m < 2 : (d) cắt (C) tại 3 điểm, (1) có 3 nghiệm.
m + 1 = 3 ⇔ m = 2 : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.
m + 1 > 3 ⇔ m > 2 : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.
a) Xét hàm số y = -x3 + 3x + 1. Tập xác định : R.
y' = -3x2 + 3 = -3(x2 - 1); y' = 0 ⇔ x = -1,x = 1.
Bảng biến thiên:
Đồ thị (C) như hình bên.
b) x3 - 3x + m = 0 ⇔ -x3 + 3x + 1 = m + 1 (1). Số nghiệm của (1) chính là số giao điểm của đồ thị (C) với đường thẳng (d) : y = m + 1.
Từ đồ thị ta thấy :
m + 1 < -1 ⇔ m < -2 : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.
m + 1 = -1 ⇔ m = -2 : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.
-1 < m + 1 < 3 ⇔ -2 < m < 2 : (d) cắt (C) tại 3 điểm, (1) có 3 nghiệm.
m + 1 = 3 ⇔ m = 2 : (d) cắt (C) tại 1 điểm và tiếp xúc với (C) tại 1 điểm, (1) có 2 nghiệm.
m + 1 > 3 ⇔ m > 2 : (d) cắt (C) tại 1 điểm, (1) có 1 nghiệm.






