Đơn giản là thế này...
\(3x^2y^2z^2+x^2y^2z^2\)
Cái \(x^2y^2z^2\) chính là 1\(x^2y^2z^2\) (Số nào nhân với 1 cũng bằng chính nó)
Vì 2 hạng tử đồng dạng nên cộng cái phần số:
\(3x^2y^2z^2+1x^2y^2z^2=4x^2y^2z^2\)
Bạn hiểu chưa?
Cho tam giác DEF có góc D=30 độ;góc E=1/2 góc F.So sánh các cạch của DEF
Cho \(\frac{x}{3}=\frac{y}{4}vs\frac{y}{5}=\frac{6}{6}\) .Tính M=\(\frac{2x+3y+4z}{3x+4y+5z}\)
Q=3x2y+3y2x tại x+-2;y=-1
A.-18
B.-9
C.18
D.12
Đố :
Tên của tác giả cuốn "Đại Việt Sử kí" dưới thời vua Trần Nhân Tông được đặt cho một đường phố của Thủ đô Hà Nội. Em sẽ biết tên tác giả đó bằng cách tính các tổng và hiệu dưới đây rồi viết chữ tương ứng vào ô dưới kết quả được cho trong bảng sau :
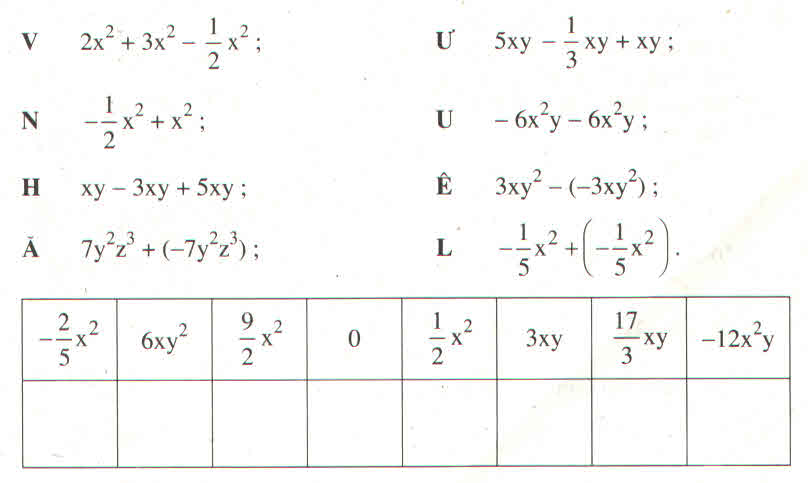
Tìm tổng của ba đơn thức :
\(25xy^2\) \(55xy^2\) \(75xy^2\)
Tìm tổng 3 đơn thức: 25xy2 ; 55xy2 và 75 xy2
Cho đồ thị hàm số: y= (m-1)/x/
a. Tìm m để đồ thị hàm số đi qua A(-1;1)
b. Vẽ đồ thị hàm số với m vừa tìm được.
c. Đường thẳng đi qua B(0;2) và cắt đồ thị hàm số tại 2 điểm M và N (M nằm bên trái trục tung). Tính MN và diện tích tam giác OMN.
Khẳng định nào sau đây là sai ?
(A) \(3x^2y^3\) và \(3x^3y^2\) là hai đơn thức đồng dạng
(B) \(-3x^2y^3\) và \(3x^2y^3\) là hai đơn thức đồng dạng
(C) \(\left(xy\right)^2\) và \(3x^2y^2\) là hai đơn thức đồng dạng
(D) \(-2\left(xy\right)^3\) và \(5x^3y^3\) là hai đơn thức đồng dạng
Cho M=\(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}\)với a;b;c >0
a)CM: M>1
b)CM: M ko là số nguyên
Khi thao luan nhom bạn Sơn nói:
0,9xy^2 va 0,9x^2y là 2 đơn thức đồng dạng, bạn Phúc nói 2 đơn thức tren ko đồng dạng
