Violympic toán 9
Các câu hỏi tương tự
1.rút gọn a.2sqrt{20}+sqrt{5}-2sqrt{45}
b.tìm điều kiện xác định và rút gọn Aleft(frac{sqrt{x}-2}{sqrt{x}+2}+frac{8sqrt{x}-3}{x-4}right):frac{1}{sqrt{x}-2}
2 cho biết a2+sqrt{3}và b2-sqrt{3}.tính giá trị biểu thức pa+b-ab
7..tínhsqrt{20}-sqrt{45}+3sqrt{18}+sqrt{72}
b.tìm điều kiện xác định và rút gọn Pleft(frac{asqrt{a}-1}{a-sqrt{a}}-frac{asqrt{a}-1}{a+sqrt{a}}right):frac{a+2}{a-2}
Đọc tiếp
1.rút gọn a.\(2\sqrt{20}+\sqrt{5}-2\sqrt{45}\)
b.tìm điều kiện xác định và rút gọn A=\(\left(\frac{\sqrt{x}-2}{\sqrt{x}+2}+\frac{8\sqrt{x}-3}{x-4}\right):\frac{1}{\sqrt{x}-2}\)
2 cho biết a=\(2+\sqrt{3}\)và b=\(2-\sqrt{3}\).tính giá trị biểu thức p=a+b-ab
7..tính\(\sqrt{20}-\sqrt{45}+3\sqrt{18}+\sqrt{72}\)
b.tìm điều kiện xác định và rút gọn P=\(\left(\frac{a\sqrt{a}-1}{a-\sqrt{a}}-\frac{a\sqrt{a}-1}{a+\sqrt{a}}\right):\frac{a+2}{a-2}\)
BÀI 3: Cho biểu thức a/ Tìm điều kiện xác định của Ab/ Rút gọn biểu thức A.c/ Tính giá trị của A tại x 25
Đọc tiếp
BÀI 3: Cho biểu thức 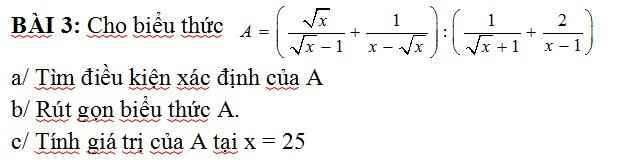
a/ Tìm điều kiện xác định của A
b/ Rút gọn biểu thức A.
c/ Tính giá trị của A tại x = 25
Cho biểu thức P = \(\left(\dfrac{4a}{\sqrt{a}-1}-\dfrac{\sqrt{a}}{a-\sqrt{a}}\right).\dfrac{\sqrt{a}-1}{a^2}\) với a>0 và a \(\ne\)1
a)Rút gọn biểu thức P b)Với giá trị nào của a thì P = 3
Tính giá trị của biểu thức: \(M=\dfrac{1+ab}{a+b}-\dfrac{1-ab}{a-b}\) với \(b=\dfrac{3\sqrt{8}-2\sqrt{12}+\sqrt{20}}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}\)
Cho biểu thức : P = \(\left(\dfrac{1}{1-\sqrt{a}}-\dfrac{1}{1+\sqrt{a}}\right).\left(\dfrac{1}{\sqrt{a}}+1\right)\) với a >0 và a \(\ne\)1
a)Rút gọn biểu thức P b)Với những giá trị nảo của a thì P >\(\dfrac{1}{2}\)
Tính giá trị của biểu thức: \(M=\dfrac{1+ab}{a+b}-\dfrac{1-ab}{a-b}\) với \(b=\dfrac{3\sqrt{8}-2\sqrt{12}+\sqrt{20}}{3\sqrt{18}-2\sqrt{27}+\sqrt{45}}\); \(a=\sqrt{4+\sqrt{8}}.\sqrt{2+\sqrt{2+\sqrt{2}}}.\sqrt{2-\sqrt{2+\sqrt{2}}}\)
Rút gọn và tìm điều kiện xác định:
\(\left(\dfrac{\sqrt{a^3}+\sqrt{b^3}}{\sqrt{a}+\sqrt{b}}-\sqrt{ab}\right):\left(a-b\right)+\dfrac{2\sqrt{b}}{\sqrt{a}+\sqrt{b}}\)
Cho biểu thức \(M=\dfrac{a\sqrt{a}-b\sqrt{b}}{a-b}-\dfrac{a}{\sqrt{a}+\sqrt{b}}-\dfrac{b}{\sqrt{b}-\sqrt{a}}\) với a,b>0 và \(a\ne b\) . Rút gọn M và tính giá trị biểu thức M biết \(\left(1-a\right).\left(1-b\right)+2\sqrt{ab}=1\)
Cho biểu thức: \(M=\sqrt{\dfrac{a-b}{a+b}}\) (ĐKXĐ: \(b^2\ne0;a^2>b^2\))
a) Tính giá trị M nếu \(\dfrac{a}{b}=\dfrac{3}{2}\)
b) Tìm điều kiện của a, b để M<1





