

c:
Xét tứ giác BKMC có \(\widehat{BKM}=\widehat{BCM}=\widehat{KMC}=90^0\)
nên BKMC là hình chữ nhật
=>BK=MC
Ta có: AK+KB=AB
DM+MC=DC
mà KB=MC và AB=DC
nên AK=DM
Xét ΔCMB vuông tại C và ΔBCA vuông tại B có
\(\widehat{CMB}=\widehat{BCA}\left(=90^0-\widehat{HBC}\right)\)
Do đó: ΔCMB~ΔBCA
=>\(\dfrac{CM}{BC}=\dfrac{CB}{BA}\)
mà CM=KB
nên \(\dfrac{KB}{BC}=\dfrac{BC}{AB}\)
=>\(\dfrac{KI}{AB}=\dfrac{BC}{AB}\)
Xét ΔABC có KI//BC
nên \(\dfrac{AK}{AB}=\dfrac{KI}{BC}\)
=>\(\dfrac{AK}{KI}=\dfrac{AB}{BC}\)
=>\(\dfrac{KI}{KA}=\dfrac{BC}{AB}\)
=>\(\dfrac{KI}{KA}=\dfrac{KB}{AD}\)
mà AK=DM
nên \(\dfrac{KI}{DM}=\dfrac{KB}{DA}\)
Xét ΔDMA vuông tại D và ΔKIB vuông tại K có
\(\dfrac{KI}{DM}=\dfrac{KB}{DA}\)
Do đó: ΔDMA~ΔKIB
=>\(\widehat{DMA}=\widehat{KIB}\)
mà \(\widehat{AMC}=180^0-\widehat{DMA};\widehat{BIM}=180^0-\widehat{KIB}\)
nên \(\widehat{AMC}=\widehat{BIM}\)















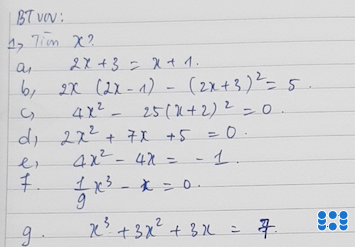

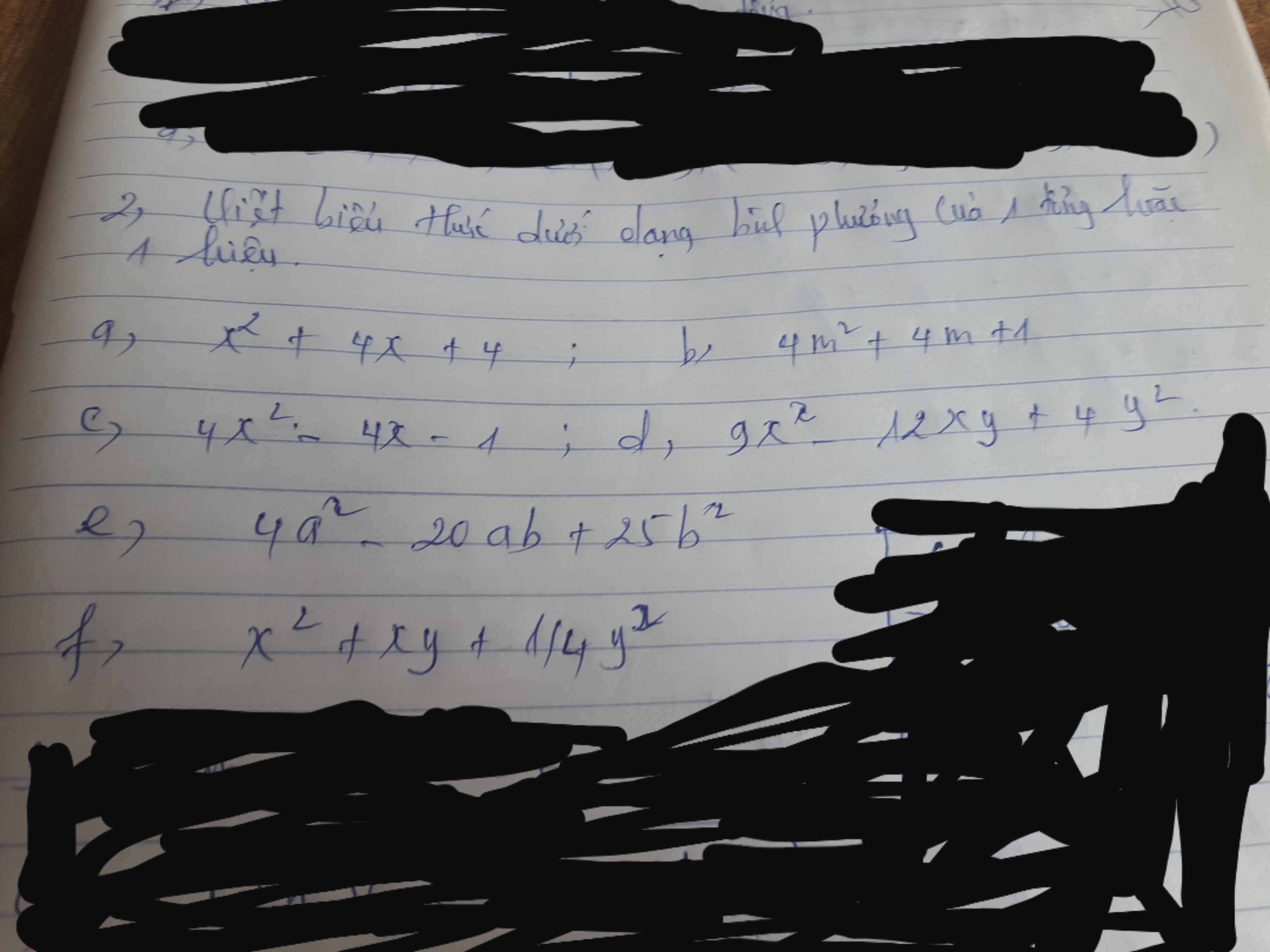



 giải thích giùm mình với
giải thích giùm mình với