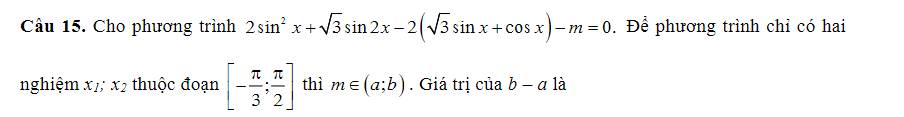Đặt \(\sqrt{3}sinx+cosx=2sin\left(x+\dfrac{\pi}{6}\right)=t\in\left[-2;2\right]\)
\(x\in\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\Rightarrow x+\dfrac{\pi}{6}\in\left[-\dfrac{\pi}{3};\dfrac{2\pi}{3}\right]\)
\(\Rightarrow t^2=3sin^2x+cos^2x+2\sqrt{3}sinx.cosx=2sin^2x+\sqrt{3}sin2x+1\)
Pt trở thành:
\(t^2-1-2t-m=0\Rightarrow t^2-2t-1=m\) (1)
Từ đường tròn lượng giác, các trường hợp thỏa mãn:
TH1: (1) có 2 nghiệm thỏa mãn: \(\left\{{}\begin{matrix}\sqrt{3}\le t_1< 2\\\left[{}\begin{matrix}t_2>2\\t_2< -\sqrt{3}\end{matrix}\right.\end{matrix}\right.\)
TH2: (1) có 2 nghiệm pb sao cho \(-\sqrt{3}\le t_1< t_2\le\sqrt{3}\)
Tới đây dùng đồ thị là xong thôi