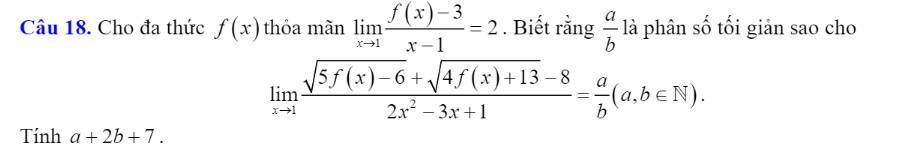Giới hạn \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-3}{x-1}\) hữu hạn \(\Rightarrow f\left(1\right)=3\)
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{5f\left(x\right)-6}-3+\sqrt{4f\left(x\right)+13}-5}{\left(x-1\right)\left(2x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{5\left[f\left(x\right)-3\right]}{\sqrt{5f\left(x\right)-6}+3}+\dfrac{4\left[f\left(x\right)-3\right]}{\sqrt{4f\left(x\right)+13}+5}}{\left(x-1\right)\left(2x-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{f\left(x\right)-3}{x-1}.\dfrac{5}{\sqrt{5f\left(x\right)-6}+3}+\dfrac{f\left(x\right)-3}{x-1}.\dfrac{4}{\sqrt{4f\left(x\right)+13}+5}}{2x-1}\)
\(=\dfrac{2.\dfrac{5}{\sqrt{5.3-6}+3}+2.\dfrac{4}{\sqrt{4.3+13}+5}}{2.1-1}=...\)