Lời giải:
Giả sử sau ít nhất x tháng thì người đó thu được cả gốc lẫn lãi 225 triệu.
Ta có:
$200(1+0,58:100)^x=225$
$200.1,0058^x=225$
$1,0058^x=1,125$
$x=\log_{1,0058}(1,125)\approx 21$ (tháng)
Đáp án B.
Diện tích hình phẳng giới hạn bởi đường thẳng y=x+3 , đường cong y=x^2+1 là
\(log_{\sqrt{3}}\left(\sqrt[5]{3}\right)=?\)
\(log_24.log_{\dfrac{1}{4}}2=?\)
\(log_5\left(\dfrac{1}{25}\right).log_{27}9=?\)
\(log_24.log_{\dfrac{1}{4}}2=?\)
a.c giúp em với ạ
thank trước ạ
cho hình chữ nhật ABCD, MN lần lượt là trung điểm của AB và DC. kẻ MP vuông góc AC tại P. Chứng minh góc BPN = 90 độ.
Tích phân từ 1 đến 2 căn bậc 2 của x +1 dx
Cho hình thanh cong (H) giới hạn bởi các đường y=e^x ,y=0,x=0,x=ln4.đường thẳng x=k (0<k<ln4) chia (H) thành 2 phần có diện tích S1,S2 như hình vẽ bên.gọi X là tập họp tất cả các giá trị k để S1^2+S2^2=5 .tổng các phần tử của X bằng
Cho tam giác ABC có các góc đều nhọn và AB<ÁC tia phân giác của góc A cắt BC . Vẽ BE vuông góc với AD tại E .Tia BE cắt ÁC tại F
a)Chứng minh rằng AB=AF
b) Qua F vẽ đường thẳng song song BC cắt AE tại H lấy điểm K nằm giữa D và C sao cho FH=DK chứng minh rằng DH =KF và DH //KF Chứng minh rằng tam giác ABC >tam giác ACB
cho hình nón có bán kính là r và độ dài đường sinh là l . diện tích xung quanh \(S_{xq}\) của hình nón bằng bao nhiêu.
Cho tam giác vuông OPM có cạnh OP nằm trên trục Ox. Đặt \(\widehat{POM}=\alpha;OM=R\left(0\le\alpha\le\dfrac{\pi}{3};R>0\right)\)
Gọi V là khối tròn xoay thu được khi quay tam giác đó xung quanh trục Ox (H.63)
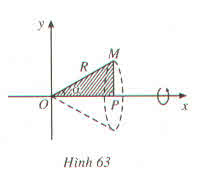
a) Tính thể tích của V theo \(\alpha\) và R
b) Tìm \(\alpha\) sao cho thể tích của V lớn nhất
cho hình phẳng h được giới hạn bởi đồ thị hàm số y = e mũ 2x trục Ox Oy và đường thẳng x = 2 tính s hình phẳng trên
