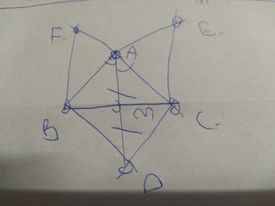
a: ΔABC cân tại A
mà AM là đường phân giác
nên AM\(\perp\)BC và M là trung điểm của BC
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: BF//AM
AM\(\perp\)BC
Do đó: BF\(\perp\)BC
=>ΔBFC vuông tại B
\(\widehat{ABC}+\widehat{ABF}=\widehat{FBC}=90^0\)
\(\widehat{ACB}+\widehat{AFB}=90^0\)(ΔBFC vuông tại B)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABF}=\widehat{AFB}\)
=>AB=AF
mà AB=AC
nên AF=AC
=>A là trung điểm của CF
AM\(\perp\)BC
EC//AM
Do đó: CE\(\perp\)CB
=>ΔCBE vuông tại C
\(\widehat{ACB}+\widehat{ACE}=\widehat{ECB}=90^0\)
\(\widehat{ABC}+\widehat{AEC}=90^0\)(ΔECB vuông tại C)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ACE}=\widehat{AEC}\)
=>AC=AE
mà AB=AC
nên AB=AE
=>A là trung điểm của BE
\(BE=2BA\)
CF=2CA
mà BA=CA
nên BE=CF
Xét tứ giác BCEF có
A là trung điểm chung của BE và CF
=>BCEF là hình bình hành
Hình bình hành BCEF có BE=CF
nên BCEF là hình chữ nhật
c: Để hình thoi ABDC là hình vuông thì \(\widehat{BAC}=90^0\)