a: a không chia hết cho 3 nên a=3k+1 hoặc a=3k+2
TH1: a=3k+1
\(a^2-1=\left(3k+1\right)^2-1\)
\(=9k^2+6k+1-1=9k^2+6k=3\left(3k^2+2k\right)⋮3\)
=>\(a^2\) chia 3 dư 1
TH2: a=3k+2
\(a^2-1=\left(3k+2\right)^2-1\)
\(=9k^2+12k+4-1\)
\(=9k^2+12k+3\)
\(=3\left(3k^2+4k+1\right)⋮3\)
=>a2 chia 3 dư 1
b: \(x^2+y^2-6x+10y+34=0\)
=>\(x^2-6x+9+y^2+10y+25=0\)
=>\(\left(x-3\right)^2+\left(y+5\right)^2=0\)
mà \(\left\{{}\begin{matrix}\left(x-3\right)^2>=0\forall x\\\left(y+5\right)^2>=0\forall y\end{matrix}\right.\)
nên \(\left\{{}\begin{matrix}x-3=0\\y+5=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=-5\end{matrix}\right.\)
c: \(A=n^3+3n^2+2n\)
\(=n\cdot\left(n^2+3n+2\right)\)
\(=n\left(n+1\right)\left(n+2\right)\)
Vì n;n+1;n+2 là ba số nguyên liên tiếp
nên \(n\left(n+1\right)\left(n+2\right)⋮3!=6\)
=>A chia hết cho 6
d: xy-5x=7
=>x(y-5)=7
=>\(\left(x;y-5\right)\in\left\{\left(1;7\right);\left(7;1\right);\left(-1;-7\right);\left(-7;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(1;12\right);\left(7;6\right);\left(-1;-2\right);\left(-7;4\right)\right\}\)
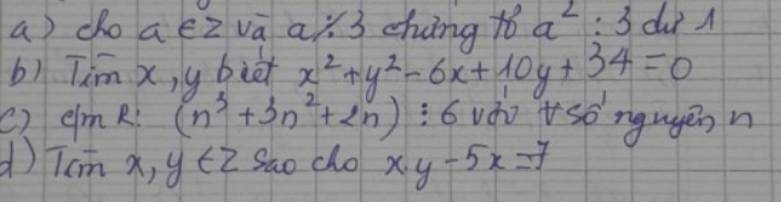
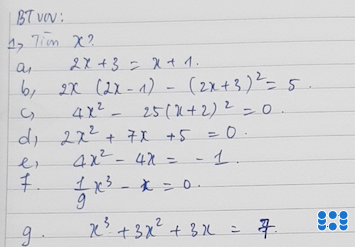
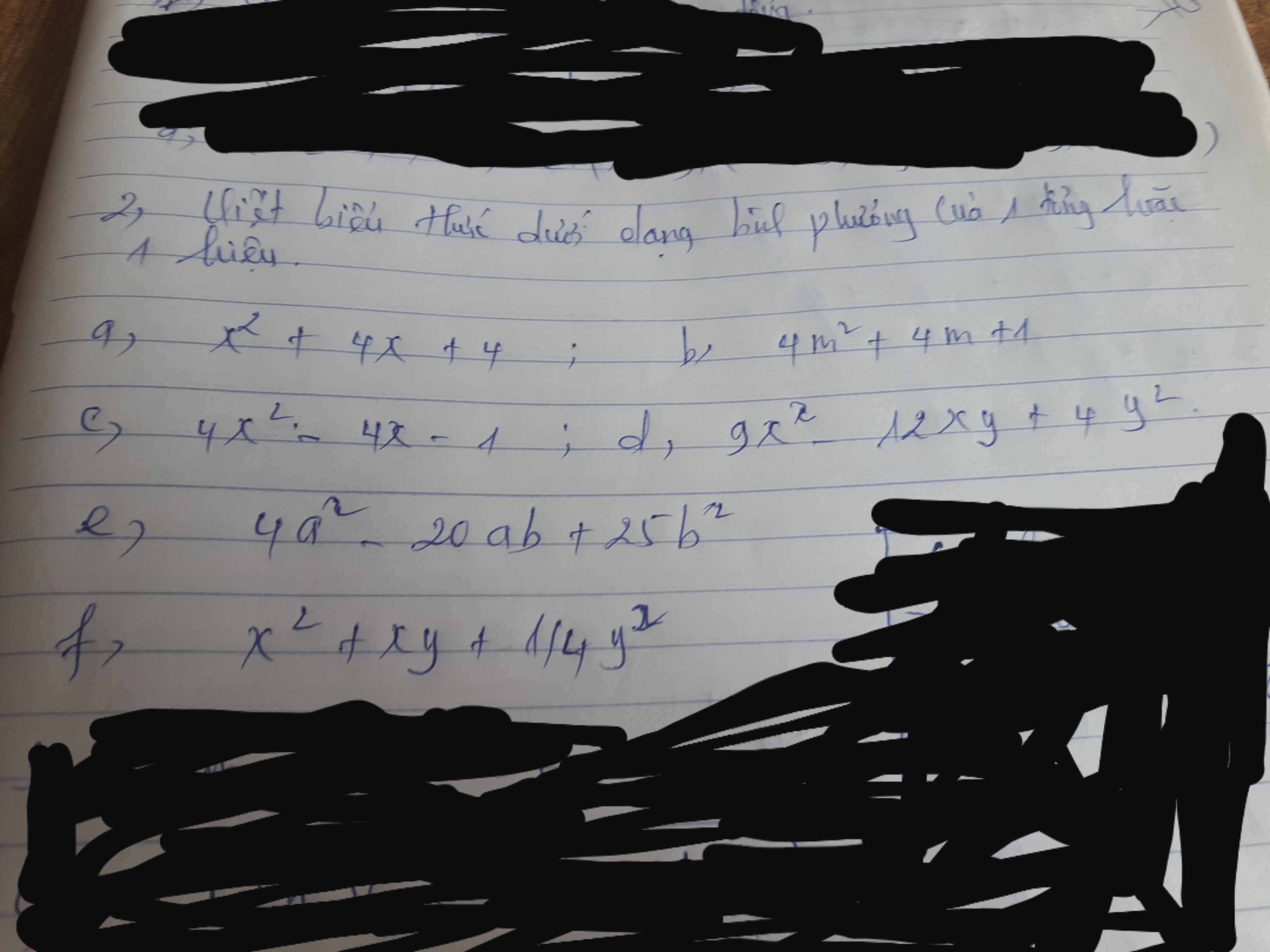
giải thích giùm mình với