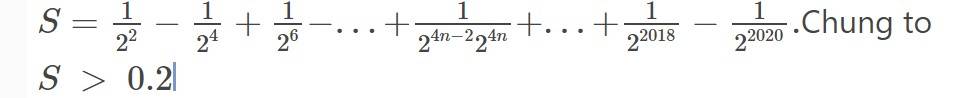Question

Answer 1

`S=1/(2^2)-1/(2^4)+1/(2^6)-...+1/(2^(4n-2)2^(4n))+...+1/(2^2018)-1/(2^2020)`

`S=1/(2^2)-1/(2^4)+1/(2^6)-...+1/(2^(4n-2))-1/(2^(4n))+...+1/(2^2018)-1/(2^2020)`

`2^2S=2^2(1/(2^2)-1/(2^4)+1/(2^6)-...+1/(2^(4n-2))-1/(2^(4n))+...+1/(2^2018)-1/(2^2020))`

`4S=1-1/(2^2)+1/(2^4)-1/(2^6)+...-1/(2^(4n-2))+1/(2^(4n))-...-1/(2^2018)`

`4S+S=(1-1/(2^2)+1/(2^4)-1/(2^6)+...-1/(2^(4n-2))+1/(2^(4n))-...-1/(2^2018))+(1/(2^2)-1/(2^4)+1/(2^6)-...+1/(2^(4n-2))-1/(2^(4n))+...+1/(2^2018)-1/(2^2020))`

`5S=1-1/(2^2020)`

`=>S=(1-1/(2^2020)):5`

`=>S=1:5-1/(2^2020):5`

`=>S=1/5-1/(2^2020) .1/5`

`=>S=1/5-1/(2^2020. 5)<1/5`

`=>S<0,2(đpcm)`

Answer 2

\(S=\dfrac{1}{2^2}-\dfrac{1}{2^4}+\dfrac{1}{2^6}-...+\dfrac{1}{2^{2018}}-\dfrac{1}{2^{2020}}\)

=>\(4S=1-\dfrac{1}{2^2}+\dfrac{1}{2^4}-...+\dfrac{1}{2^{2016}}-\dfrac{1}{2^{2018}}\)

=>\(5S=1-\dfrac{1}{2^{2020}}\)

=>\(S=\dfrac{1}{5}-\dfrac{1}{5\cdot2^{2020}}< \dfrac{1}{5}=0.2\)