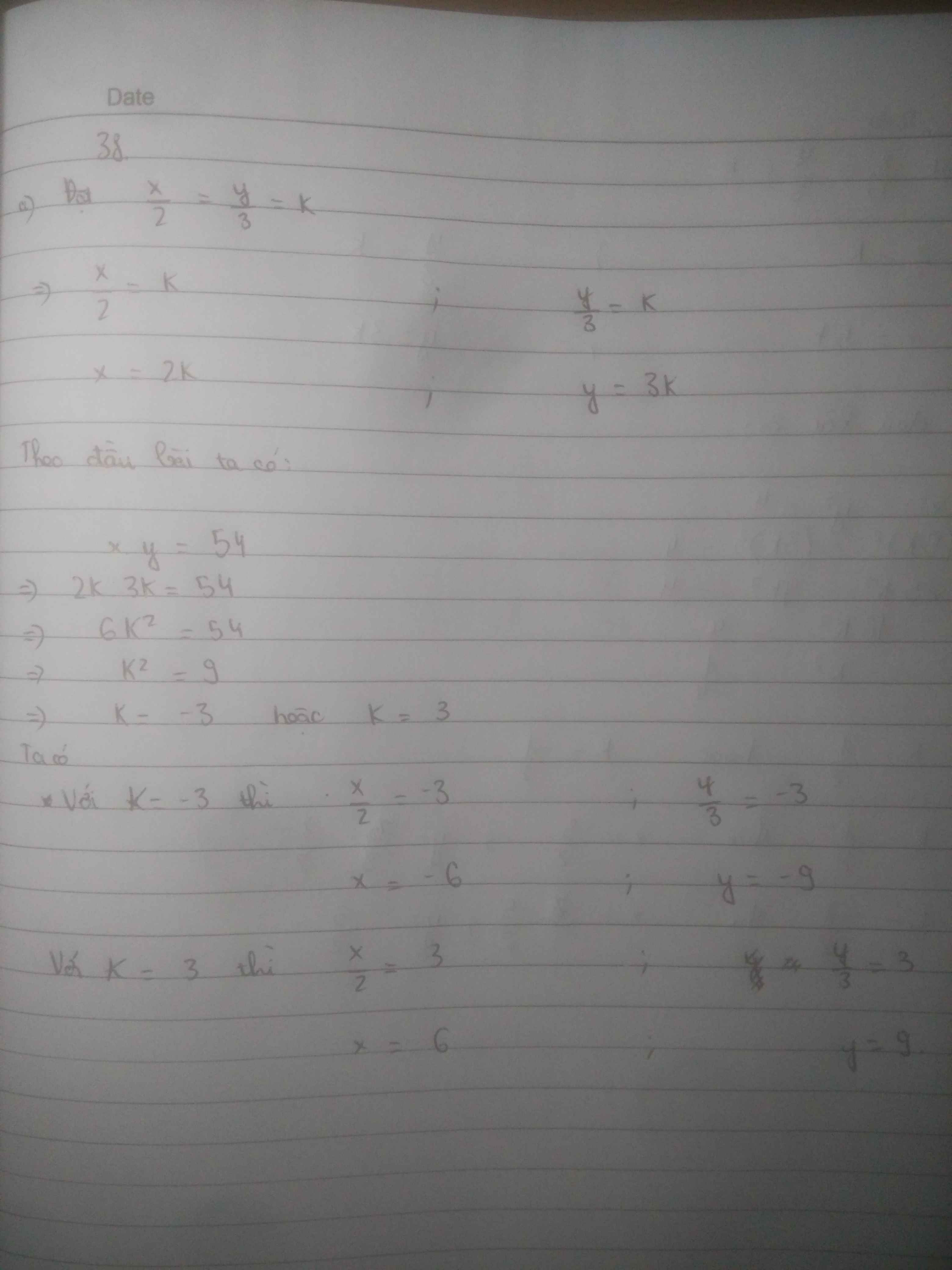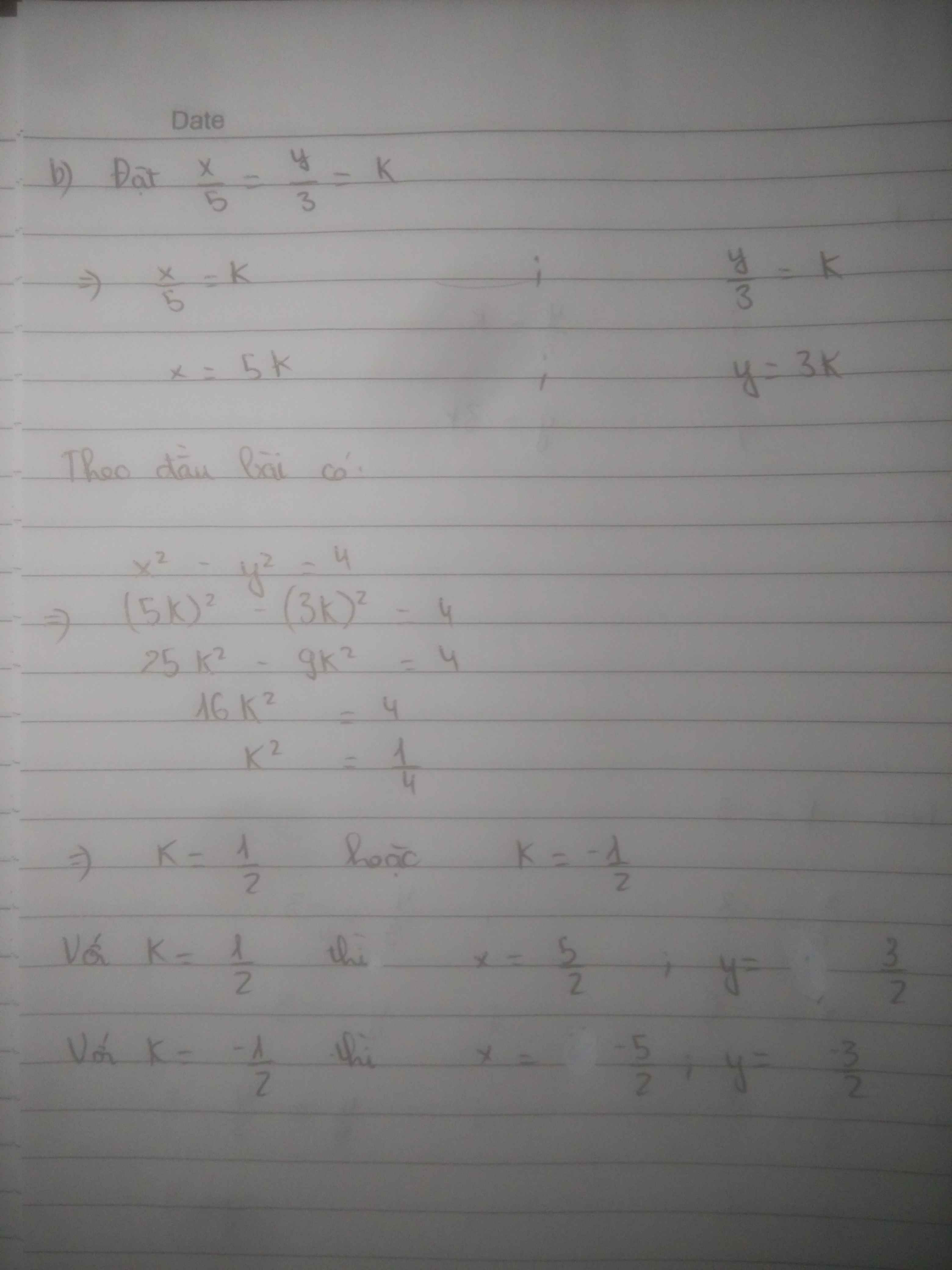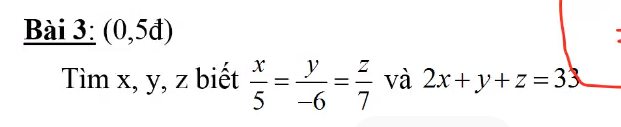a, Đặt \(x=2k;y=3k\)
Ta có : \(xy=54\Rightarrow6k^2=54\Leftrightarrow k^2=9\Leftrightarrow k=\pm3\)
Với k = 3 thì x = 6 ; y = 9
Với k = -3 thì x = -6 ; y = -9
b, Áp dụng tính chất dãy tỉ số bằng nhau
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{x^2-y^2}{25-9}=\dfrac{4}{16}=\dfrac{1}{4}\Rightarrow x=\dfrac{5}{4};y=\dfrac{3}{4}\)
a) Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2k\\y=3k\end{matrix}\right.\)
Ta có: xy=54
\(\Leftrightarrow6k^2=54\)
\(\Leftrightarrow k^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}k=3\\k=-3\end{matrix}\right.\)
Trường hợp 1: k=3
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\cdot3=6\\y=3\cdot3=9\end{matrix}\right.\)
Trường hợp 2: k=-3
\(\Leftrightarrow\left\{{}\begin{matrix}x=2\cdot\left(-3\right)=-6\\y=2\cdot\left(-3\right)=-9\end{matrix}\right.\)
b) Đặt \(\dfrac{x}{5}=\dfrac{y}{3}=k\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5k\\y=3k\end{matrix}\right.\)
Ta có: \(x^2-y^2=4\)
\(\Leftrightarrow\left(5k\right)^2-\left(3k\right)^2=4\)
\(\Leftrightarrow25k^2-9k^2=4\)
\(\Leftrightarrow k^2=\dfrac{1}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}k=\dfrac{1}{2}\\k=-\dfrac{1}{2}\end{matrix}\right.\)
Trường hợp 1: \(k=\dfrac{1}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\cdot\dfrac{1}{2}=\dfrac{3}{2}\\y=5\cdot\dfrac{1}{2}=\dfrac{5}{2}\end{matrix}\right.\)
Trường hợp 2: \(k=-\dfrac{1}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\cdot\dfrac{-1}{2}=\dfrac{-3}{2}\\y=5\cdot\dfrac{-1}{2}=\dfrac{-5}{2}\end{matrix}\right.\)