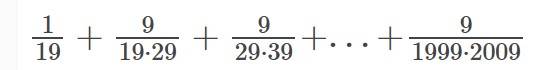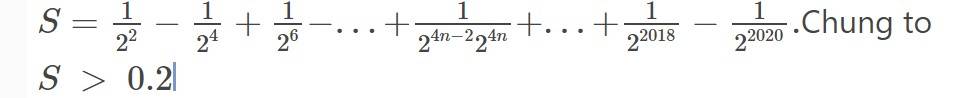\(\dfrac{1}{19}+\dfrac{9}{19\cdot29}+\dfrac{9}{29\cdot39}+...+\dfrac{9}{1999\cdot2009}\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\left(\dfrac{10}{19\cdot29}+\dfrac{10}{29\cdot39}+...+\dfrac{10}{1999\cdot2009}\right)\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\left(\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{39}+...+\dfrac{1}{1999}-\dfrac{1}{2009}\right)\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\cdot\left(\dfrac{1}{19}-\dfrac{1}{2009}\right)\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\cdot\dfrac{1990}{19\cdot2009}\)
\(=\dfrac{1}{19}+\dfrac{199\cdot9}{19\cdot2009}\)
\(=\dfrac{2009+199\cdot9}{19\cdot2009}=\dfrac{3800}{19\cdot2009}=\dfrac{200}{2009}\)
\(=\dfrac{1}{19}+\dfrac{9}{10}.\dfrac{29-19}{19.29}+\dfrac{9}{10}.\dfrac{39-29}{29.39}+.....+\dfrac{9}{10}.\dfrac{2009-1999}{1999.2009}\\ =\dfrac{1}{19}+\dfrac{9}{10}\left(\dfrac{10}{19.29}+\dfrac{10}{29.39}+....+\dfrac{10}{1999.2009}\right)\\ =\dfrac{1}{19}+\dfrac{9}{10}.\left(\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{39}+....+\dfrac{1}{1999}-\dfrac{1}{2009}\right)\\ =\dfrac{1}{19}+\dfrac{9}{10}.\left(\dfrac{1}{19}-\dfrac{1}{2009}\right)\)
\(=\dfrac{1}{19}+\dfrac{9}{10}\times\dfrac{1990}{38171}=\dfrac{1}{19}+\dfrac{1791}{39171}=\dfrac{200}{2009}\)
\(\dfrac{1}{19}+\dfrac{9}{19\cdot29}+\dfrac{9}{29\cdot39}+...+\dfrac{9}{1999\cdot2009}\)
\(=\dfrac{9}{9\cdot19}+\dfrac{9}{19\cdot29}+\dfrac{9}{29\cdot39}+...+\dfrac{9}{1999\cdot2009}\)
\(=\dfrac{9}{10}\cdot\left(\dfrac{10}{9\cdot19}+\dfrac{10}{19\cdot29}+\dfrac{10}{29\cdot39}+...+\dfrac{10}{1999\cdot2009}\right)\)
\(=\dfrac{9}{10}\cdot\left(\dfrac{1}{9}-\dfrac{1}{19}+\dfrac{1}{19}-\dfrac{1}{29}+\dfrac{1}{29}-\dfrac{1}{39}+...+\dfrac{1}{1999}-\dfrac{1}{2009}\right)\)
\(=\dfrac{9}{10}\cdot\left(\dfrac{1}{9}-\dfrac{1}{2009}\right)\)
\(=\dfrac{9}{10}\cdot\dfrac{2800}{18081}\)
\(=\dfrac{200}{2009}\)
\(Toru\)