Vd8:
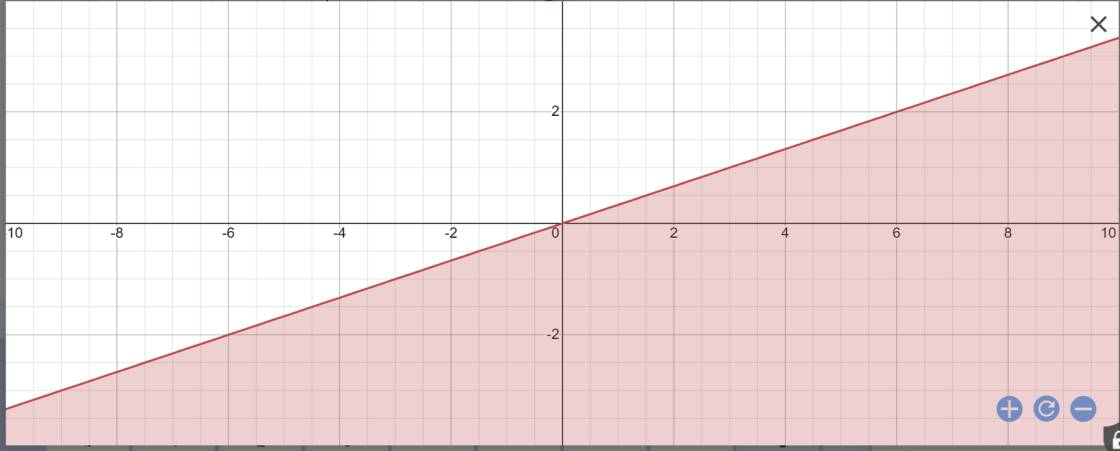
a: x-3y>=0
=>3y<=x
=>y<=x/3
Đặt (d): y=x/3
Thay x=0 và y=0 vào BPT y<=x/3, ta được:
\(0< =\dfrac{0}{3}=0\)(đúng)
Vậy: Miền nghiệm của BPT x-3y>=0 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
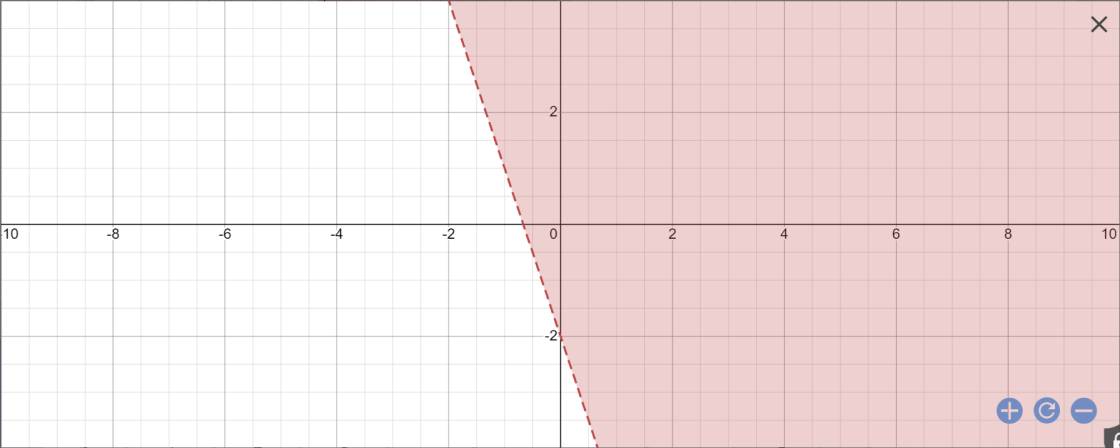
b: \(\dfrac{x-y}{-2}< x+y+1\)
=>\(-\dfrac{1}{2}x+\dfrac{1}{2}y< x+y+1\)
=>\(-\dfrac{1}{2}x+\dfrac{1}{2}y-x-y< 1\)
=>\(-\dfrac{3}{2}x-\dfrac{1}{2}y< 1\)
=>\(-3x-y< 2\)
Gọi (d1): -3x-y=2
=>y=-3x-2
Thay x=0 và y=0 vào BPT -3x-y<2, ta được:
\(-3\cdot0-0< 2\)
=>0<2(đúng)
Vậy: Miền nghiệm của bất phương trình \(\dfrac{x-y}{-2}< x+y+1\) là nửa mặt phẳng không chứa biên nhưng chưa điểm O(0;0)