§2. Hàm số y=ax+b
Nội dung lý thuyết
I. ÔN TẬP VỀ HÀM SỐ BẬC NHẤT
\(y=ax+b\left(a\ne0\right)\)
Tập xác định: \(D=R\)
Chiều biến thiên:
Với \(a>0\) hàm số đồng biến trên \(R\).
Với \(a< 0\) hàm số nghịch biến trên \(R\).
Ví dụ:
+) Hàm số \(y=\dfrac{1}{2}x-3\) đồng biến trên \(R\) (do \(\dfrac{1}{2}>0\))
+) Hàm số \(y=-3x+\dfrac{5}{6}\) nghịch biến trên \(R\) (do \(-3< 0\))
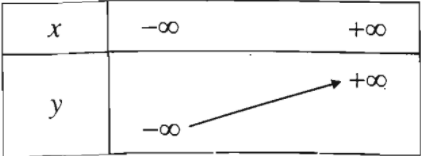
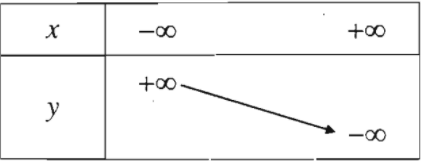
Bảng biến thiên:
| \(a>0\) | \(a< 0\) |
|
|
Đồ thị:
Đồ thị của hàm số là một đường thẳng không song song và cũng không trùng với các trục tọa độ. Đường thẳng này luôn song song với đường thẳng \(y=ax\) (nếu \(b\ne0\)) và đi qua 2 điểm \(A\left(0;b\right)\) và \(B\left(-\dfrac{b}{a};0\right)\).
+) Với \(a< 0\):
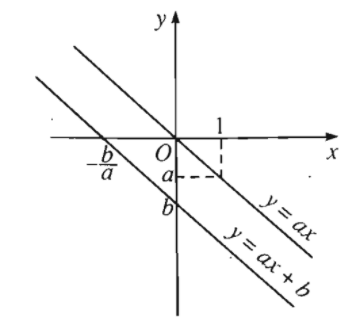
+) Với \(a>0\):

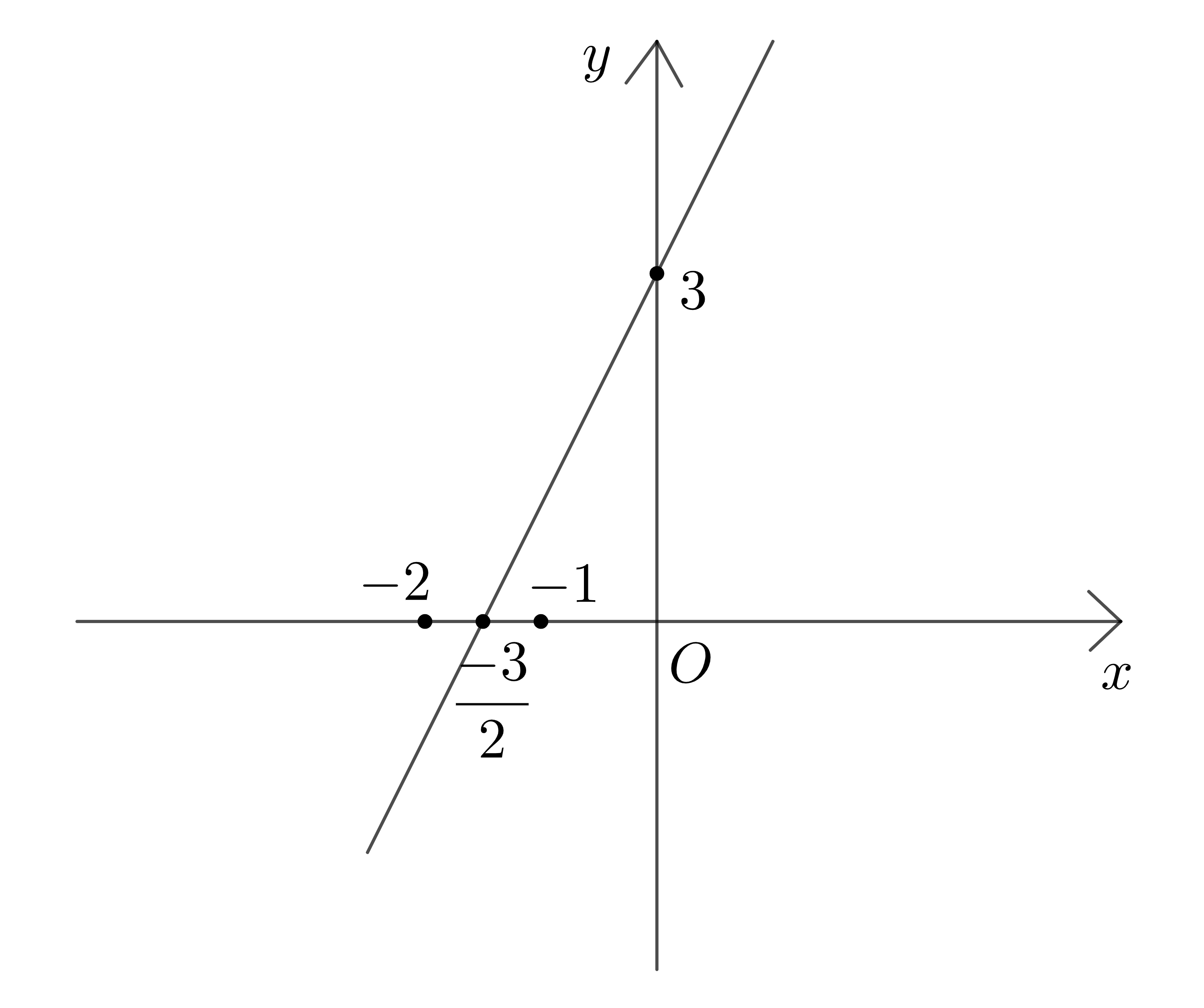
Ví dụ 1: Vẽ đồ thị hàm số \(y=2x+3\).
Ta thấy:
Do \(2>0\) nên hàm số \(y=2x+3\) đồng biến trên \(R\).
Đồ thị hàm số đi qua hai điểm là \(A\left(0;3\right)\) và \(B\left(-\dfrac{3}{2};0\right)\).
Ta có đồ thị hàm số như sau:
Ví dụ 2. Cho hàm số \(y=\left(m-3\right)x+m^2+1\). Xác định giá trị của tham số m để hàm số luôn nghịch biến trên \(R\).
Giải:
Để hàm số \(y=\left(m-3\right)x+m^2+1\) luôn nghịch biến trên \(R\)
\(\Leftrightarrow m-3< 0\)
\(\Leftrightarrow m< 3\)
Vậy các giá trị của m cần tìm là \(m< 3\).
@70508@
Ví dụ 3: Xác định các hệ số \(a,b\) sao cho đồ thị hàm số \(y=ax+b\) đi qua 2 điểm \(A\left(1;3\right)\) và \(B\left(-2;4\right)\).
Giải:
Do đồ thị hàm số \(y=ax+b\) đi qua \(A\left(1;3\right)\) và \(B\left(-2;4\right)\). Nên thay tọa độ của A và B vào phương trình đường thẳng ta được hệ phương trình: \(\left\{{}\begin{matrix}3=a+b\\4=-2a+b\end{matrix}\right.\)
Giải hệ phương trình trên ta được \(\left\{{}\begin{matrix}a=-\dfrac{1}{3}\\b=\dfrac{10}{3}\end{matrix}\right.\)
@1870431@
II. HÀM SỐ HẰNG \(y=b\)
Ví dụ: Xét hàm số hằng \(y=2\):
Với \(x=1\), giá trị của hàm số là \(y=2\) ;
Với \(x=-3,2\), giá trị của hàm số là \(y=2\) ;
Với \(x=\dfrac{4}{5}\), giá trị của hàm số là \(y=2\) ;
Với \(x=0\), giá trị của hàm số là \(y=2\) ; ....
Ta thấy: Với mọi giá trị của \(x\), giá trị của hàm số luôn luôn là \(y=2\).
Nhận xét:
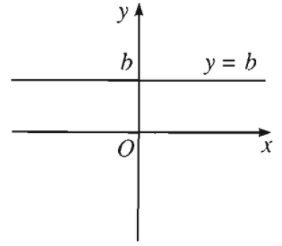
Đồ thị của hàm số \(y=b\) là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung tại điểm \(\left(0;b\right)\). Đường thẳng này gọi là đường thẳng \(y=b\).
III. HÀM SỐ \(y=\left|x\right|\)
Hàm số \(y=\left|x\right|\) có liên quan chặt chẽ với hàm bậc nhất.
1. Tập xác định
Hàm số \(y=\left|x\right|\) xác định với mọi giá trị của \(x\), tức là tập xác định \(D=R\).
2. Chiều biến thiên
Theo định nghĩa của giá trị tuyệt đối ta có:
\(y=\left|x\right|=\left\{{}\begin{matrix}x\left(x\ge0\right)\\-x\left(x< 0\right)\end{matrix}\right.\)
Từ đó suy ra:
Hàm số \(y=\left|x\right|\) nghịch biến trên khoảng \(\left(-\infty;0\right)\) và đồng biến trên khoảng \(\left(0;+\infty\right)\).
Bảng biến thiên:
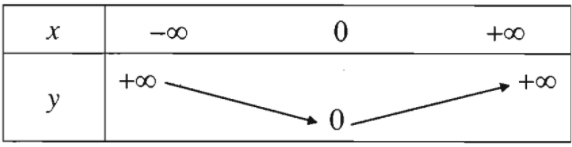
Khi \(x>0\) và dần tới \(+\infty\) thì \(y=x\) dần tới \(+\infty\)
Khi \(x< 0\) và dần tới \(-\infty\) thì \(y=-x\) cũng dần tới \(+\infty\).
Ta có bảng biến thiên sau:
3. Đồ thị hàm số
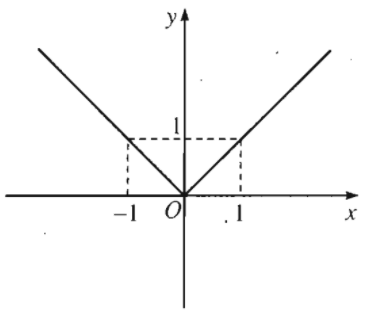
Trong nửa khoảng \([0;+\infty)\) đồ thị của hàm số \(y=\left|x\right|\) trùng với đồ thị của hàm số \(y=x\);
Trong khoảng \(\left(-\infty;0\right)\) đồ thị của hàm số \(y=\left|x\right|\) trùng với đồ thị của hàm số \(y=-x\).
Chú ý: Hàm số \(y=\left|x\right|\) là một hàm số chẵn, đồ thị của nó nhận \(Oy\) làm trục đối xứng.
@1871122@