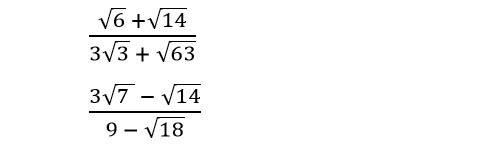a: \(=\dfrac{\sqrt{2}\left(\sqrt{3}+\sqrt{7}\right)}{3\left(\sqrt{3}+\sqrt{7}\right)}=\dfrac{\sqrt{2}}{3}\)
b: \(=\dfrac{\sqrt{7}\left(3-\sqrt{2}\right)}{3\left(3-\sqrt{2}\right)}=\dfrac{\sqrt{7}}{3}\)
a) \(\dfrac{\sqrt{6}+\sqrt{14}}{3\sqrt{3}+\sqrt{63}}\)
\(=\dfrac{\sqrt{2}\cdot\sqrt{3}+\sqrt{2}\cdot\sqrt{7}}{3\sqrt{3}+3\sqrt{7}}\)
\(=\dfrac{\sqrt{2}\cdot\left(\sqrt{3}+\sqrt{7}\right)}{3\cdot\left(\sqrt{3}+\sqrt{7}\right)}\)
\(=\dfrac{\sqrt{2}}{3}\)
b) \(\dfrac{3\sqrt{7}-\sqrt{14}}{9-\sqrt{18}}\)
\(=\dfrac{3\sqrt{7}-\sqrt{2}\cdot\sqrt{7}}{9-3\sqrt{2}}\)
\(=\dfrac{\sqrt{7}\cdot\left(3-\sqrt{2}\right)}{3\cdot\left(3-\sqrt{2}\right)}\)
\(=\dfrac{\sqrt{7}}{3}\)