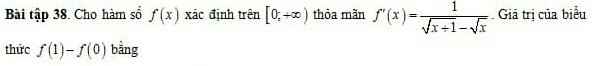\(f\left(1\right)-f\left(0\right)=\int_0^1\dfrac{1}{\sqrt{x+1}-\sqrt{x}}dx\)
\(=\int_0^1\left(\sqrt{x+1}+\sqrt{x}\right)dx\)
\(=\left(\dfrac{2}{3}.\left(x+1\right)^{\dfrac{3}{2}}+\dfrac{2}{3}.\left(x\right)^{\dfrac{3}{2}}\right)|_0^1\)
\(=\dfrac{2}{3}\left(2^{\dfrac{3}{2}}+1\right)-\dfrac{2}{3}\)
\(=\dfrac{2}{3}\left(\sqrt{8}+1\right)-\dfrac{2}{3}=\dfrac{4\sqrt{2}}{3}\)
Giải giúp ạ 
Tính nguyên hàm \(I=\int\frac{x^4+x^2+1}{x\left(x-2\right)\left(x+2\right)}\)
Câu này làm như thế nào ạ?
Đề: Tìm nguyên hàm F(x) của hàm số f(x)=(4x+1)sin2x.
tìm nguyên hàm của y=xsinx
tìm a, b sao cho F(x) = (a sin x + b cos x ) .ex là một nguyên hàm của f(x) = ex .cos x trên R
Cho hình chóp S.ABC Có đáy ABC là tam giác vuông tại B,AB=a ,Góc ACB =30 độ .SA vuông góc với mặt phẳng đáy .cạnh bên SC tạo với đáy một góc 60 độ
a .tính theo a thể tích khối chóp S.ABC
b. Tính khoảng cách từ điểm A đến mặt phẳng (SBC)
c. Tính khoảng cách từ M đến (SBC) với M là điểm trên AB sao cho AM =2MB
d. tính khoảng cách giữa hai đường thẳng CM và SB
tính nguyên hàm của e\(^{x^2}\)
Tìm nguyên hàm \(I=\frac{x^2+3x-1}{x^3+4x^2+4x}dx\)
cho hàm số \(f\left(x\right)=\dfrac{\left(sinx+2x\right)\left[\left(x^2+1\right)sinx-x\left(cosx+2\right)\right]}{\left(cosx+2\right)^2\sqrt{\left(x^2+1\right)^3}}\). Biết F(x) là một nguyên hàm của f(x) và F(0)=2021. Tính giá trị biểu thức T=F(-1) + F(1).
\(\int(x)ln(x+1)dx\)
Tính nguyên hàm
