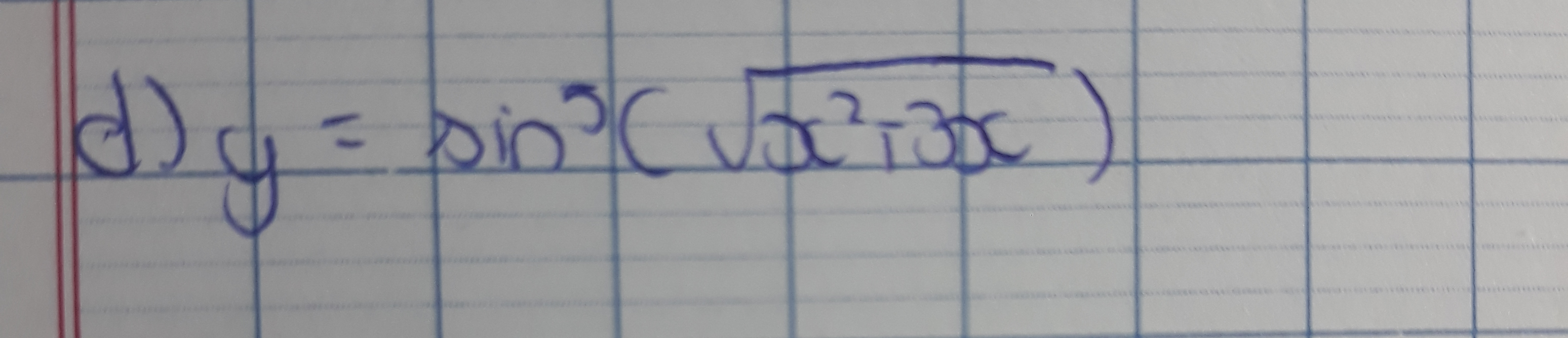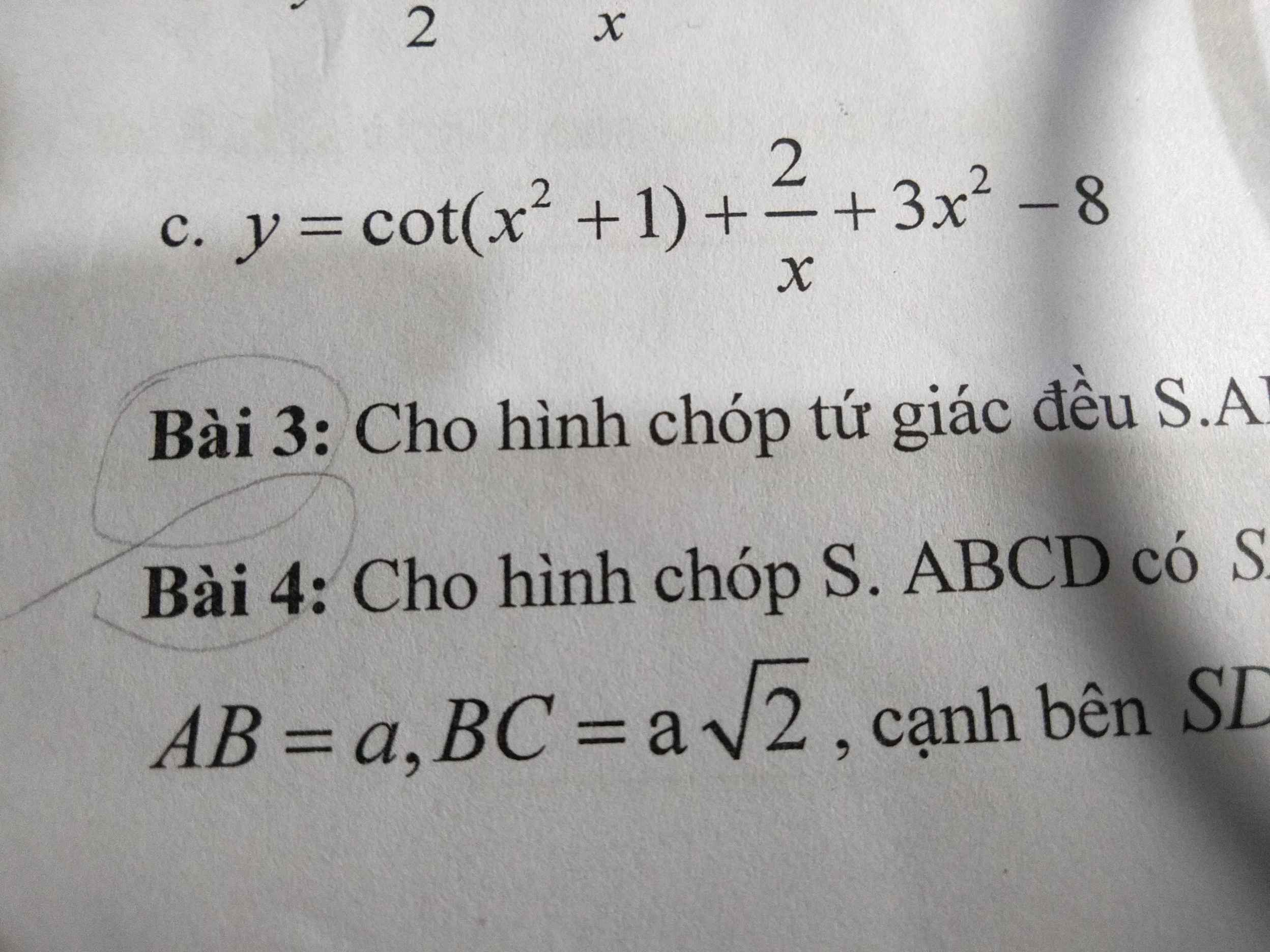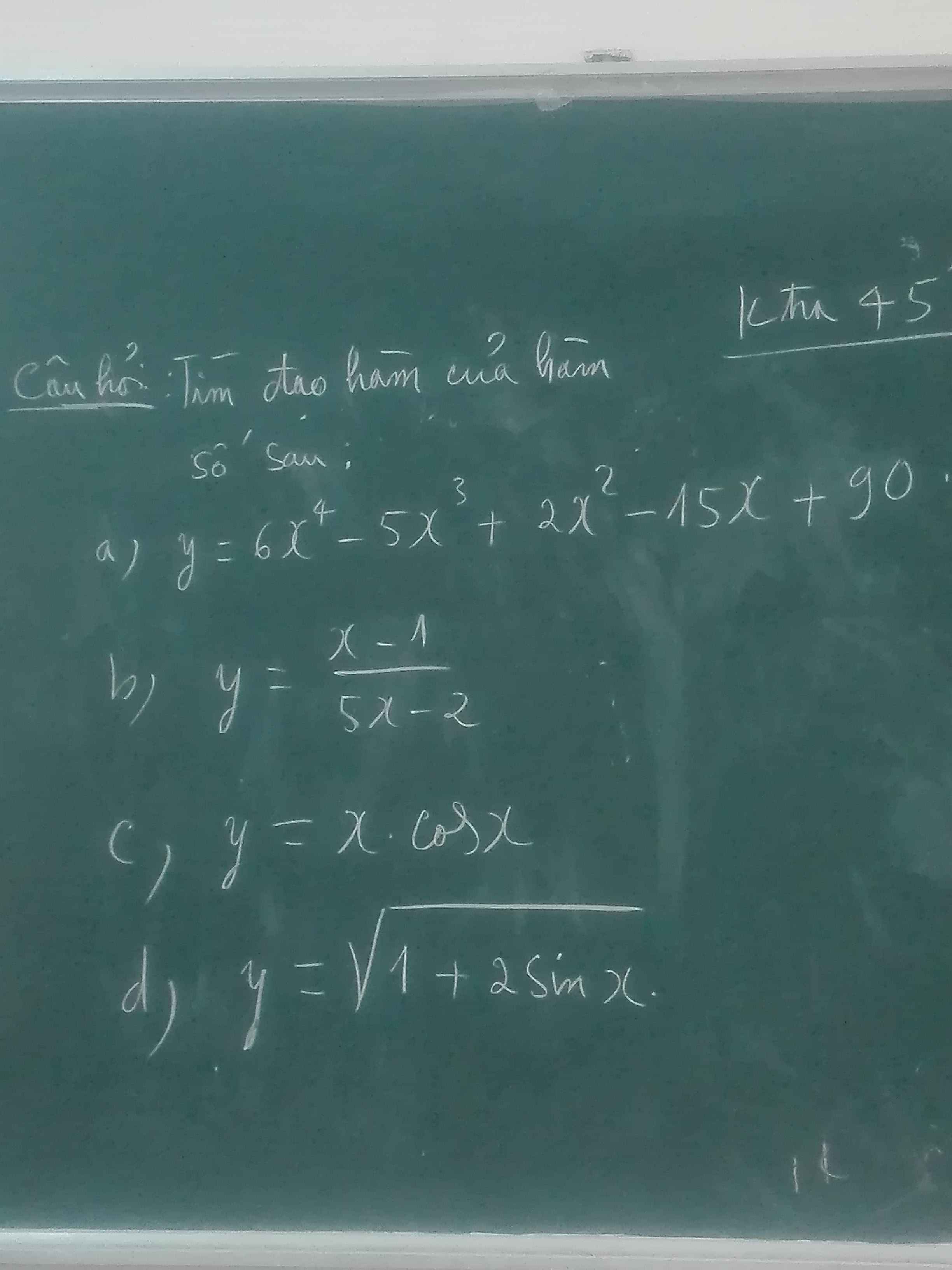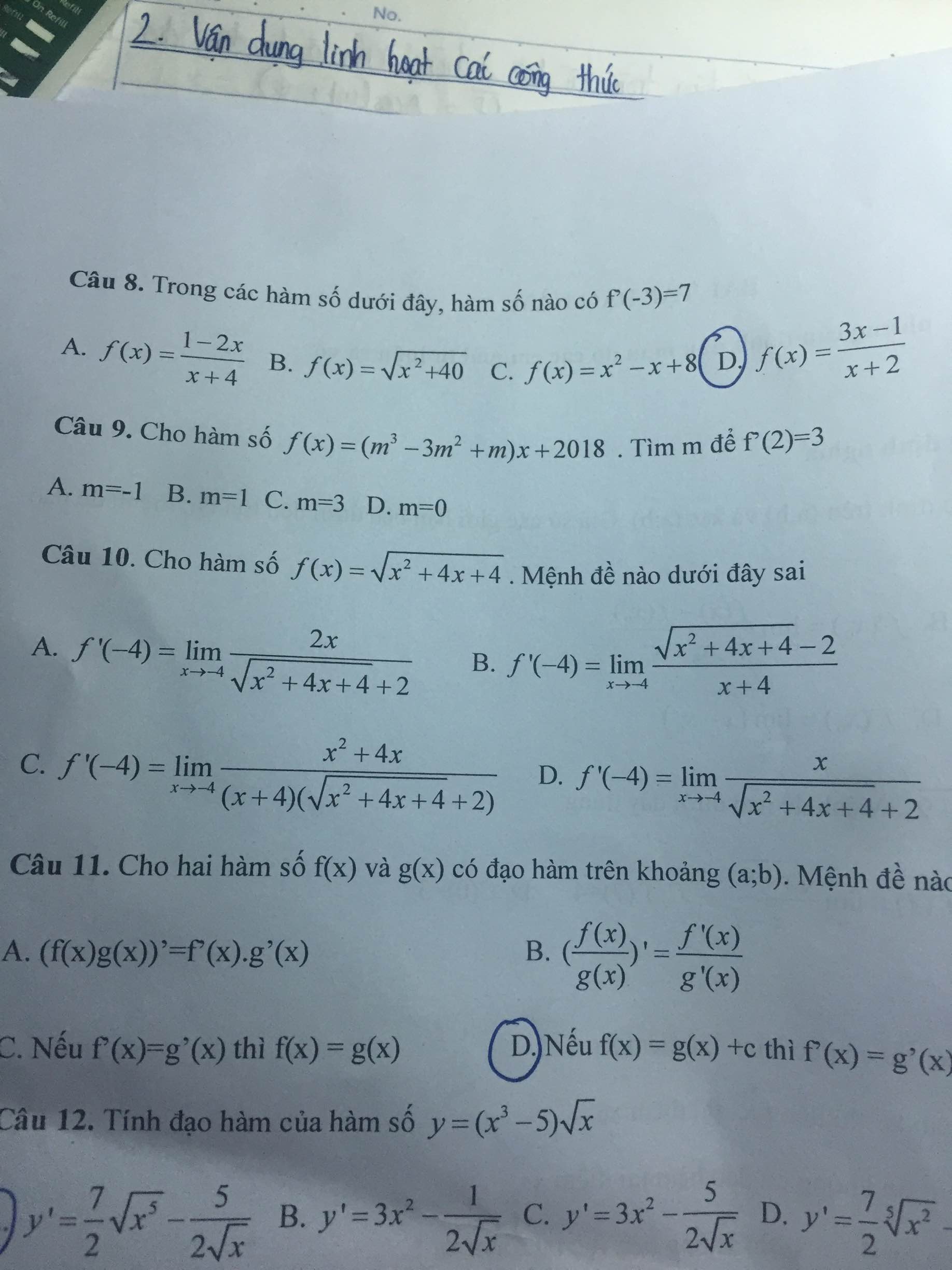Question

Answer 1

\(y^`=5\cdot sin^4\left(\sqrt{x^2+3x}\right)\cdot\left[sin\left(\sqrt{x^2+3x}\right)\right]^`\)

\(=5\cdot sin^4\left(\sqrt{x^2+3x}\right)\cdot cos\sqrt{x^2+3x}\)

Answer 2

\(y'=5\sin^4\left(\sqrt{x^2+3x}\right).\left[\sin\left(\sqrt{x^2+3x}\right)\right]'\)

\(=5\sin^4\left(\sqrt{x^2+3x}\right).\cos\left(\sqrt{x^2+3x}\right).\left(\sqrt{x^2+3x}\right)'\)

\(=5\sin^4\left(\sqrt{x^2+3x}\right)\cos\left(\sqrt{x^2+3x}\right).\dfrac{1}{2\sqrt{x^2+3x}}\left(x^2+3x\right)'\)

\(=5\sin^4\left(\sqrt{x^2+3x}\right)\cos\left(\sqrt{x^2+3x}\right).\dfrac{2x+3}{2\sqrt{x^2+3x}}\)