- \(AC=AH+HC=20+21=41\left(cm\right)\)
- \(\Delta ABH\) vuông tại H có:
\(\cos\widehat{BAH}=\dfrac{AH}{AB}\Rightarrow\cos45^0=\dfrac{AH}{AB}\)
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{\sqrt{2}}{2}\Rightarrow AB=AH\sqrt{2}=20\sqrt{2}\left(cm\right)\).
- Mặt khác, ta chứng minh được \(\Delta ABH\) vuông cân tại H do có \(\widehat{ABH}=45^0\).
\(\Rightarrow AH=BH=20\left(cm\right)\)
- \(\Delta BCH\) vuông tại H có:
\(BC^2=BH^2+CH^2\) (định lí Py-ta-go).
\(\Rightarrow BC=\sqrt{BH^2+CH^2}=\sqrt{20^2+21^2}=29\left(cm\right)\)
- Vậy: \(\left\{{}\begin{matrix}P_{ABC}=AB+BC+CA=20\sqrt{2}+29+41=70+20\sqrt{2}\left(cm\right)\\S_{ABC}=\dfrac{1}{2}BH.AC=\dfrac{1}{2}20.41=410\left(cm^2\right)\end{matrix}\right.\)
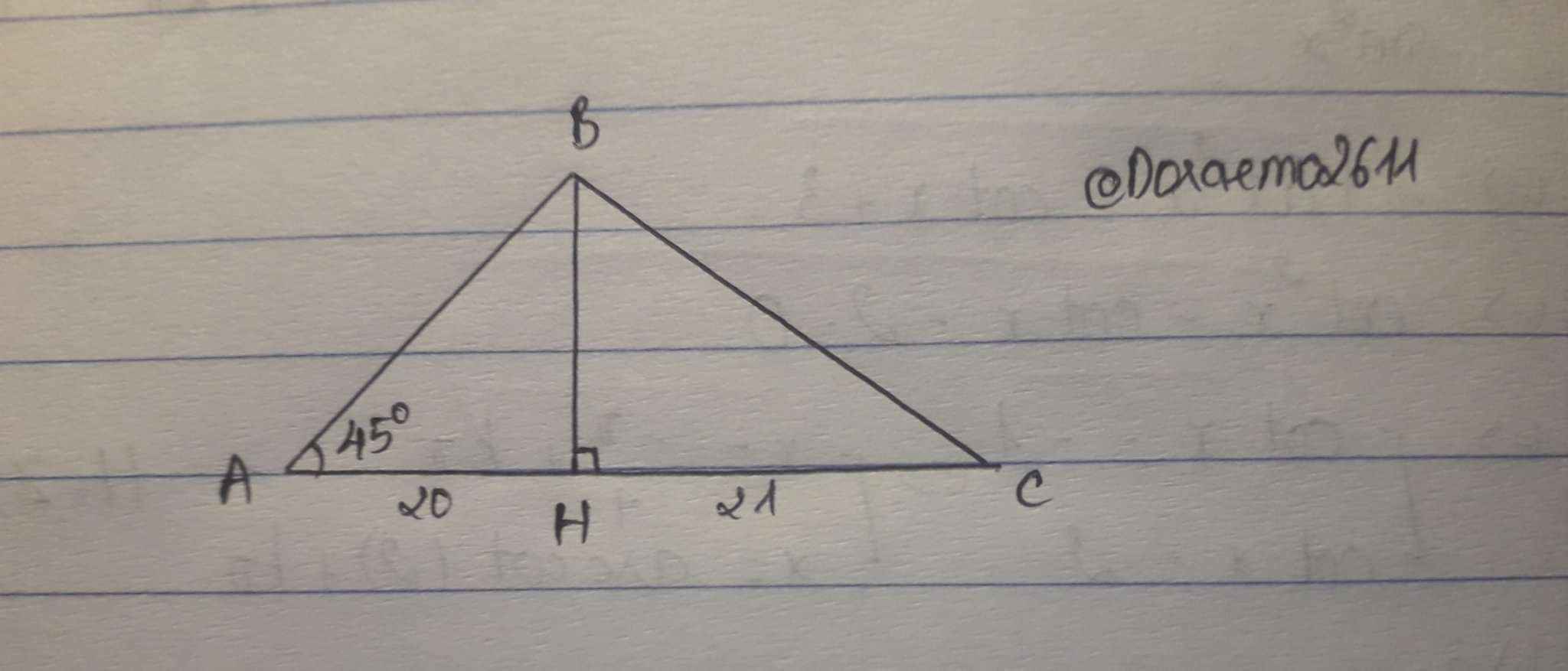
Vì `\triangle BHA` vuông tại `H` mà `\hat{A}=45^o`
`=>\triangle BHA` vuông cân tại `H`
`=>BH=AH=20(cm)`
Xét `\triangle ABH` vuông tại `H` có: `BH^2+AH^2=AB^2`
`=>20^2+20^2=AB^2=>AB=20\sqrt{2}(cm)`
Xét `\triangle BHC` vuông tại `H` có: `BH^2+HC^2=BC^2`
`=>20^2+21^2=BC^2=>BC=29(cm)`
Ta có: `AH+HC=AC=20+21=41(cm)`
`@` Chu vi `\triangle ABC` là: `AB+AC+BC=20\sqrt{2}+29+41=70+20\sqrt{2}(cm)`
`@` Diện tích `\triangle ABC` là: `1/2BH.AC=1/2 .20.41=410(cm^2)`