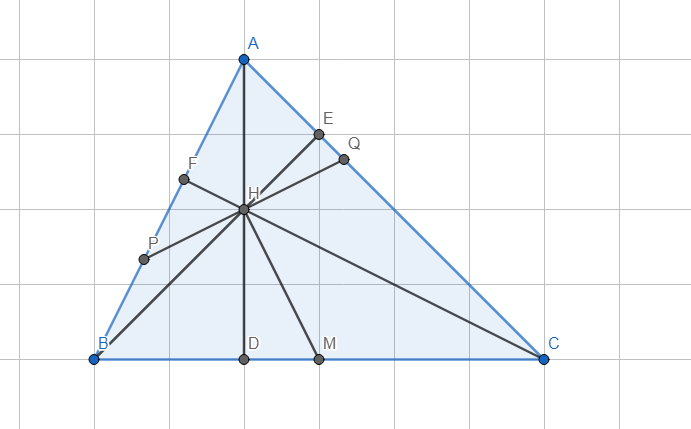
a. \(\widehat{HCM}=90^0-\widehat{CBF}=\widehat{PAH}\).
\(\widehat{HMC}=180^0-\widehat{HMD}=180^0-\left(90^0-\widehat{DHM}\right)=180^0-\widehat{PHD}=\widehat{PHA}\)
△AHP và △CMH có: \(\widehat{HCM}=\widehat{PAH};\widehat{HMC}=\widehat{PHA}\)
\(\Rightarrow\)△AHP∼△CMH (g-g).
b. △AHP∼△CMH \(\Rightarrow\dfrac{HP}{MH}=\dfrac{AH}{CM}\Rightarrow\dfrac{HP}{AH}=\dfrac{MH}{CM}\Rightarrow HP=\dfrac{MH.AH}{CM}\left(1\right)\).
c. \(\widehat{HAQ}=90^0-\widehat{ECB}=\widehat{MBH}\)
\(\widehat{AHQ}=\widehat{PHD}=90^0-\widehat{DHM}=\widehat{BMH}\)
△AHQ và △BMH có: \(\widehat{HAQ}=\widehat{MBH};\widehat{AHQ}=\widehat{BMH}\)
\(\Rightarrow\)△AHQ∼△BMH (g-g)
\(\Rightarrow\dfrac{HQ}{MH}=\dfrac{AH}{BM}\Rightarrow HQ=\dfrac{AH.MH}{BM}\left(2\right)\)
Từ (1) và (2) suy ra: \(HP=HQ\) (do BM=CM).
a) Xét hai góc nhọn APH và CHM , ta có :
\(PH\perp MH;AP\perp HC\)
Do đó \(\widehat{APH}=\widehat{MHC}\left(1\right)\)
Chứng minh tương tự :
\(\widehat{PAH}=\widehat{HCM}\left(2\right)\)
Từ (1) và (2) suy ra :
ΔAHP ∼ ΔCMH (3)
Tương tự trên ta được :
ΔQHA ∼ ΔHMB (4)
b)
Từ (3) , ta có :
\(\dfrac{HP}{MH}=\dfrac{AH}{CM}hay\dfrac{HP}{AH}=\dfrac{MH}{CM}\left(5\right)\)
c) Từ (4) , ta có : \(\dfrac{QH}{HM}=\dfrac{HA}{MB}hay\dfrac{QH}{HA}=\dfrac{MH}{MB}\) (6)
Nhưng CM = MB (7)
Từ (5) , (6) , (7) , ta suy ra : \(\dfrac{HP}{HA}=\dfrac{HQ}{HA}\) (8)
Từ (8) , ta có :
HP = HQ ( đpcm )

















