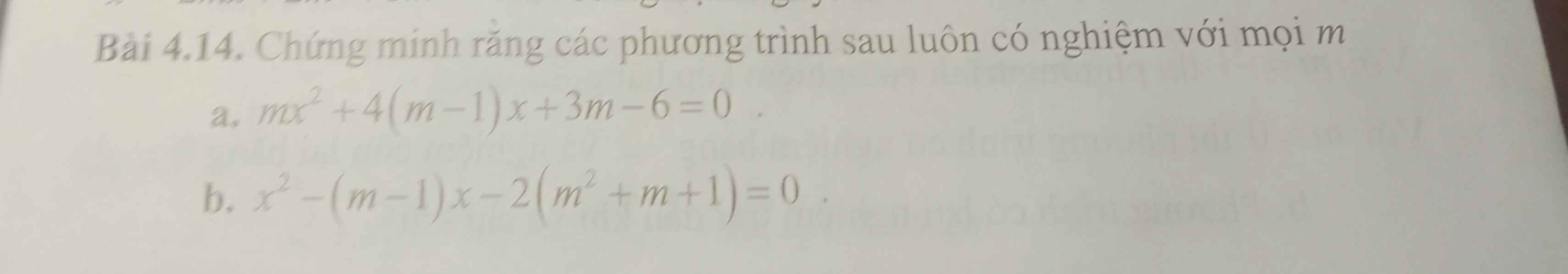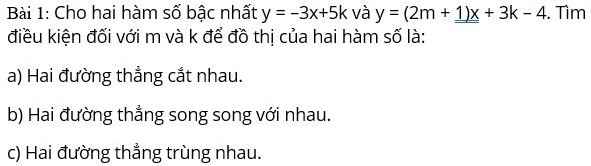Question

Answer 1

a: TH1: m=0

Pt trở thành \(4\cdot\left(0-1\right)x+3\cdot0-6=0\)

=>-4x-3=0

=>x=-3/4(nhận)

Trường hợp 2: m<>0

\(\text{Δ}=\left(4m-4\right)^2-4m\left(3m-6\right)\)

\(=16m^2-32m+16-12m^2+24m\)

\(=4m^2-8m+16\)

\(=4m^2-8m+4+12=\left(2m-2\right)^2+12>0\)

Do đó:PHương trình luôn có hai nghiệm phân biệt

b: \(\text{Δ}=\left(m-1\right)^2-4\cdot\left[-2\left(m^2+m+1\right)\right]\)

\(=m^2-2m+1+8m^2+8m+8\)

\(=9m^2+6m+9\)

\(=9m^2+6m+1+8=\left(3m+1\right)^2+8>0\)

Do đó: Phương trình luôn có hai nghiệm phân biệt