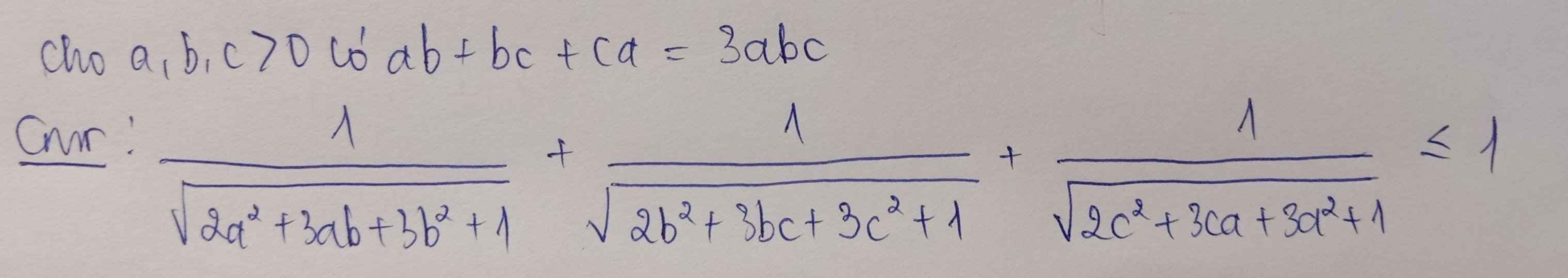Phân tích 1 chút xíu, ta cần tìm số k sao cho:
\(2a^2+3ab+3b^2-k\left(a-b\right)^2\) có thể tách về bình phương
\(\Rightarrow\left(2-k\right)a^2+\left(2k+3\right)ab+\left(3-k\right)b^2\) tách được về bình phương
Hay \(\Delta=\left(2k+3\right)^2-4\left(2-k\right)\left(3-k\right)=0\)
\(\Rightarrow k=\dfrac{15}{32}\)
Từ đó:
\(2a^2+3ab+3b^2+1=\dfrac{1}{32}\left(7a+9b\right)^2+\dfrac{15}{32}\left(a-b\right)^2+1\ge\dfrac{1}{32}\left(7a+9b\right)^2+1\)
Lại có:
\(\left[\left(7a+9b\right)^2+32\right]\left(8+1\right)\ge\left(2\sqrt{2}\left(7a+9b\right)+4\sqrt{2}\right)^2\)
\(\Rightarrow\sqrt{\dfrac{\left(7a+9b\right)^2+32}{32}}\ge\dfrac{2\sqrt{2}\left(7a+9b+2\right)}{3.\sqrt{32}}=\dfrac{7a+9b+2}{6}\)
Do đó:
\(P\le\dfrac{6}{7a+9b+2}+\dfrac{6}{7b+9c+2}+\dfrac{6}{7c+9a+2}\)
\(P\le\dfrac{6}{18^2}\left(\dfrac{7}{a}+\dfrac{9}{b}+2+\dfrac{7}{b}+\dfrac{9}{c}+2+\dfrac{7}{c}+\dfrac{9}{a}+2\right)\)
\(P\le\dfrac{6}{18^2}\left(6+\dfrac{16\left(ab+bc+ca\right)}{abc}\right)=1\)
Dấu "=" xảy ra khi \(a=b=c=1\)