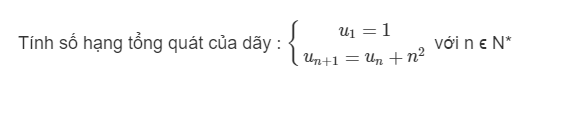\(u_{n+2}=4u_{n+1}-4u_n\)
\(\Leftrightarrow u_{n+2}-2u_{n+1}=2\left(u_{n+1}-2u_n\right)\)
Đặt \(u_{n+1}-2u_n=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_2-u_1=2\\v_{n+1}=2v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội 2
\(\Rightarrow v_n=2.2^{n-1}=2^n\)
\(\Rightarrow u_{n+1}-2u_n=2^n\)
\(\Rightarrow u_{n+1}-\dfrac{1}{2}\left(n+1\right).2^{n+1}=2\left(u_n-\dfrac{1}{2}n.2^n\right)\)
Đặt \(u_n-\dfrac{1}{2}n.2^n=x_n\Rightarrow\left\{{}\begin{matrix}x_1=u_1-1=0\\x_{n+1}=2x_n\end{matrix}\right.\)
\(\Rightarrow x_n=0.2^{n-1}=0\)
\(\Rightarrow u_n=\dfrac{1}{2}n.2^n=n.2^{n-1}\)
Đúng 1
Bình luận (0)
