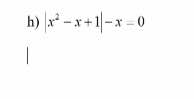\(\Leftrightarrow\left|x^2-x+1\right|=x\)
\(ĐK:x\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}-x^2+x-1=x\\x^2-x+1=x\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-x^2-1=0\left(vô.lí\right)\\x^2-2x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x=1\left(tm\right)\)
Vậy \(S=\left\{1\right\}\)
\(\left|x+2\right|+\left|x-3\right|=6\)
b) |3x – 6| = 20 – x
\(\left|x-1\right|=\left|x\left(x+1\right)\right|\)
\(\left|6-|x-2|\right|2=5x+9\)
Giải các phương trình sau :
a,\(x.\left|x+3\right|-\left|x^2+x+1\right|=1\)
b,\(\left|x\right|^3-3.\left|x\right|+2=0\)
|x-1|=|1+x|
giải phương trình trên
Giải các pt sau
a. |2x-1|=x+3
b. |x+2|=|3x-1|
c. |x+1|+|x-2|=4
giúp m giải bài 424 và 425 dùm nha
Giải các phương trình sau. a)|-2x|-x+5=1. b)x-5x+|-2x|-3=0
1.Giải bất phương trình sau:
(x-2)(x+1)<0
2. Giai phương trình:
x^2+2x+2|x+1| -2=0
Giair các phương trình sau
\(a,\left|5x\right|=x+2\) \(b,\left|7x-3\right|-2x+6=0\)
\(c,\left|2x-3\right|-21=x\) \(d,\left|9-x\right|=2x\)
\(e,\left|x-15\right|+1=3x\) \(f,\left|5-4x\right|=4-5x\)
Ai giúp mik với ạ mik đang cần gấp
