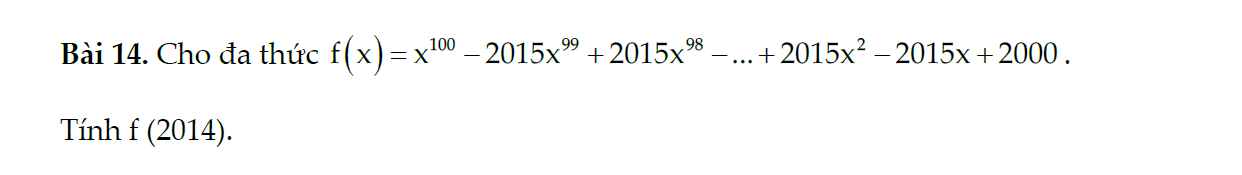\(2015=x+1\)
\(f\left(2014\right)=x^{100}-\left(x+1\right)x^{99}+\left(x+1\right)x^{98}-...+\left(x+1\right)x^2-\left(x+1\right)x+2000\)
\(=x^{100}-x^{100}-x^{99}+x^{99}+x^{98}-...+x^3+x^2-x^2-x+2000\)
\(=-x+2000=-2014+2000=-14\)
\(f\left(x\right)=x^{100}-2015x^{99}+2015x^{98}-...+2015x^2-2015x+2000\)
\(=x^{99}\left(x-2014\right)-x^{98}\left(x-2014\right)+x^{97}\left(x-2014\right)-...+x\left(x-2014\right)-x+2000\)
\(f\left(2014\right)=x^{99}\left(2014-2014\right)-x^{98}\left(2014-2014\right)+x^{97}\left(2014-2014\right)-...+x\left(2014-2014\right)-2014+2000=2000-2014=-14\)