a) ĐKXĐ: \(x\notin\left\{3;-4\right\}\)
Ta có: \(\dfrac{x+3}{x-3}+\dfrac{x-5}{x+4}=\dfrac{2x^2}{x^2+x-12}\)
\(\Leftrightarrow\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x-3\right)\left(x+4\right)}+\dfrac{\left(x-5\right)\left(x-3\right)}{\left(x+4\right)\left(x-3\right)}=\dfrac{2x^2}{\left(x+4\right)\left(x-3\right)}\)
Suy ra: \(x^2+7x+12+x^2-8x+15-2x^2=0\)
\(\Leftrightarrow27-x=0\)
hay x=27(thỏa ĐK)
Vậy: S={27}


















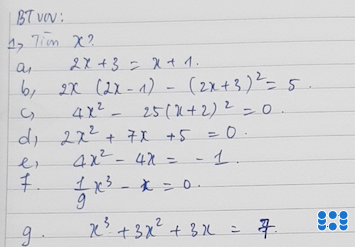

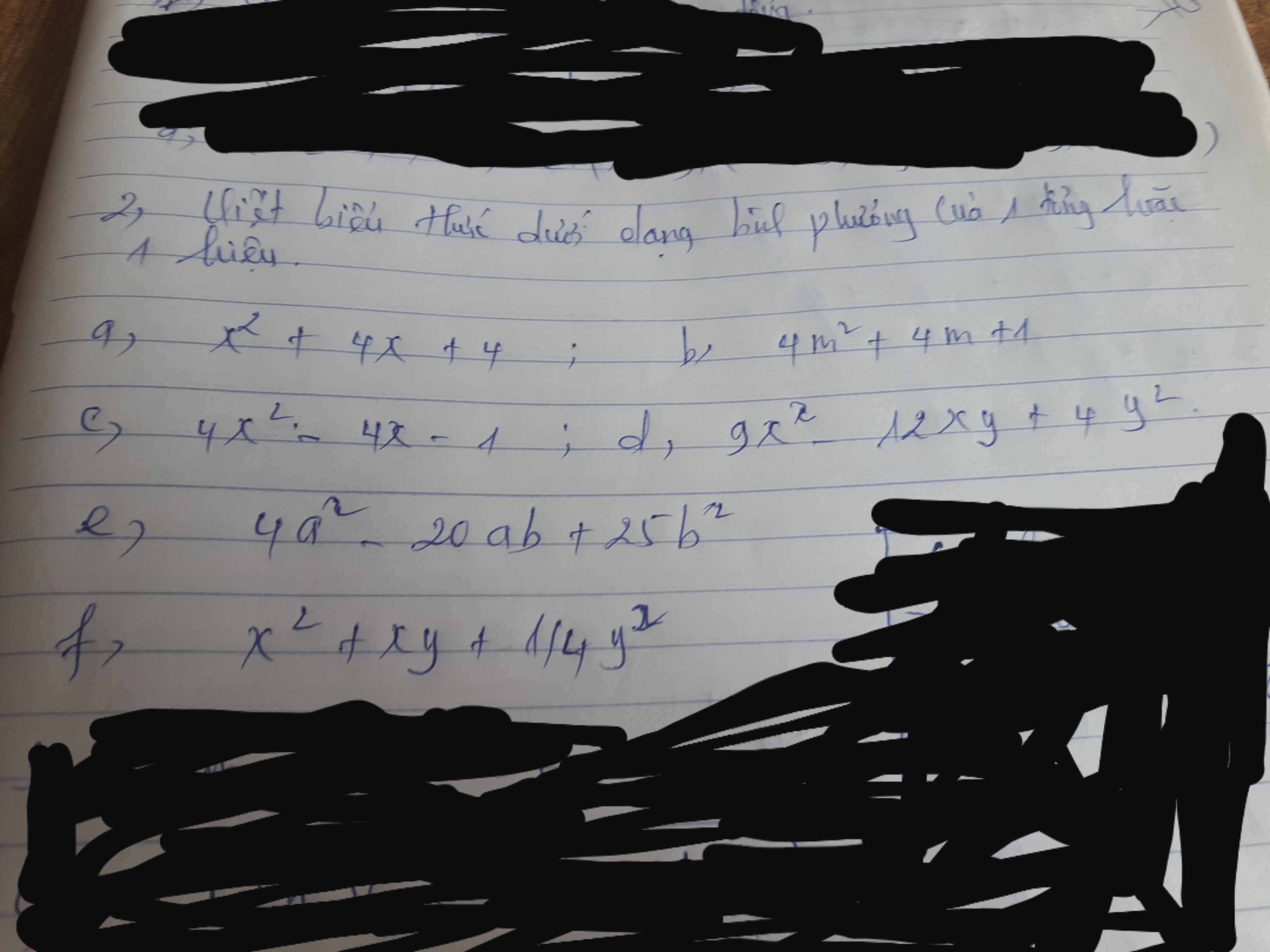



 giải thích giùm mình với
giải thích giùm mình với