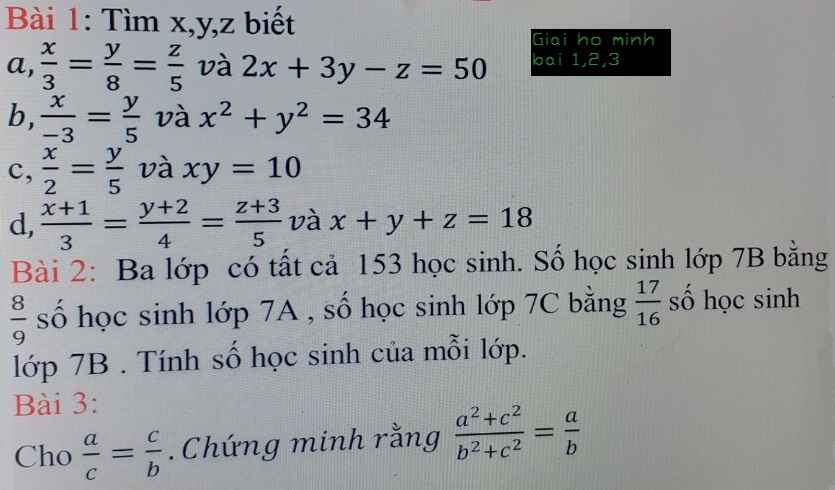
1a) Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
x/3 = y/8 = z/5 = 2x/6 = 3y/24 = z/5 = (2x + 3y - z)/(6 + 24 - 5) = 50/25 = 2
--> x = 3.2 = 6
y = 8.2 = 16
z = 5.2 = 10
b) đặt x = -3k; y = 5k
x^2 + y^2 = 34
(-3k)^2 + (5k)^2 = 34
34k^2 = 34
k^2 = 1
Khi k = 1 --> x = -3.1 = -3
y = 5.1 = 5
Khi k = -1 --> x = -3.(-1) = 3
y = 5.(-1)=-5
c) đặt x=2k; y=5k
xy=10
2k.5k=10
k^2=1
Th1: k = 1 --> x = 2.1=2
y=5.1=5
Th2: k=-1 --> x = 2.(-1)=-2
y=5.(-1)=-5
d) áp dụng tính chất dãy tỉ số bằng nhau:
(x+1)/3=(y+2)/4=(z+3)/5 = (x+y+z+6)/(3+4+5)=(18+6)/12 = 2
--> x = 3.2 - 1 = 5
y = 4.2-2=6
z=5.2-3=7
Bài 3
\(\dfrac{a}{c}=\dfrac{c}{b}\Rightarrow\dfrac{a}{c}=\dfrac{c}{b}\)
\(\Rightarrow\dfrac{a^2}{c^2}=\dfrac{c^2}{b^2}=\dfrac{a^2.c^2}{c^2.b^2}=\dfrac{a^2}{b^2}=\dfrac{a}{b}\left(1\right)\)
Áp dụng t/c của dãy số bằng nhau, ta có: \(\Rightarrow\dfrac{a^2}{c^2}=\dfrac{c^2}{b^2}=\dfrac{a^2+c^2}{c^2+b^2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\dfrac{a^2+c^2}{c^2+b^2}=\dfrac{a}{b}\)