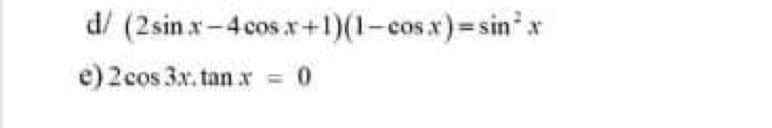d.
\(\Leftrightarrow\left(2sinx-4cosx+1\right)\left(1-cosx\right)=1-cos^2x\)
\(\Leftrightarrow\left(2sinx-4cosx+1\right)\left(1-cosx\right)=\left(1-cosx\right)\left(1+cosx\right)\)
\(\Leftrightarrow\left(1-cosx\right)\left(2sinx-5cosx\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\2sinx=5cosx\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\tanx=\dfrac{5}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=arctan\left(\dfrac{5}{2}\right)+k\pi\end{matrix}\right.\)
e.
ĐKXĐ: \(x\ne\dfrac{\pi}{2}+k\pi\)
\(\dfrac{2cos3x.sinx}{cosx}=0\)
\(\Leftrightarrow\dfrac{2\left(4cos^3x-3cosx\right)sinx}{cosx}=0\)
\(\Rightarrow\left(4cos^2x-3\right)sinx=0\)
\(\Leftrightarrow\left(2cos2x-1\right)sinx=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=0\\cos2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\pm\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)