Question

Answer 1

b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:

\(CE\cdot CA=CH^2\left(1\right)\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔDHC vuông tại H có HF là đường cao ứng với cạnh huyền DC, ta được:

\(CF\cdot CD=CH^2\left(2\right)\)

Từ (1) và (2) suy ra \(CE\cdot CA=CF\cdot CD\)

Answer 2

giúp mik câu c vs ạ

 

Answer 3

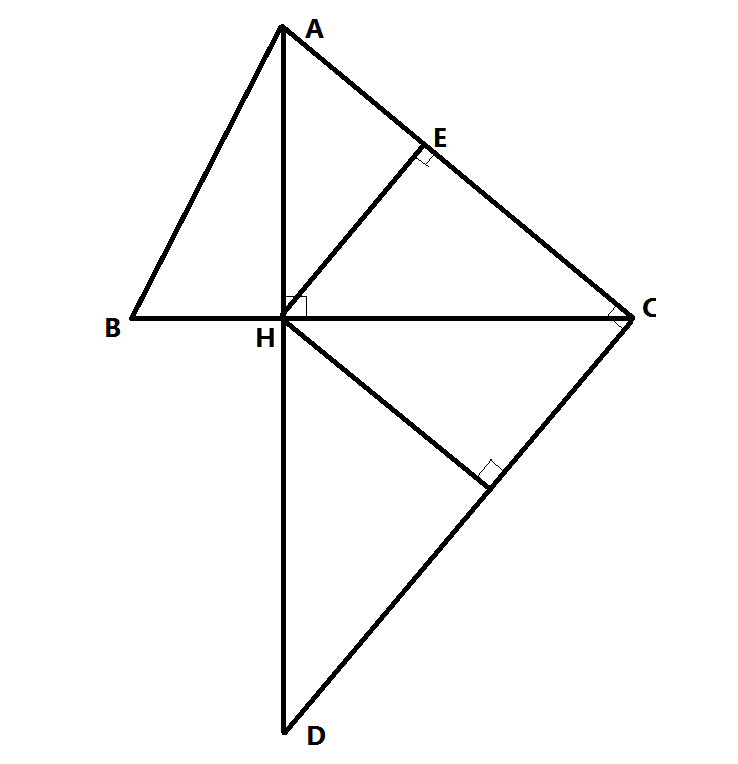
a/

+Xét △AHC vuông tại A, ta có:

AH²+HC²=AC²(Định lý Pytago)
=>HC²=AC²-AH²

=>HC²=5²-3²
=>HC=\(\sqrt{16}\)=4(cm)
+Xét △ACD vuông tại C, có CH là đường cao, ta có:
*AC²=AH.AD
=>5²=3.AD
=>AD=\(\dfrac{25}{3}\)(cm)

HD=AD-AH=\(\dfrac{25}{3}\)-3=\(\dfrac{16}{3}\)(cm)
 

*CD²=HD.AD
=>CD²=\(\dfrac{16}{3}\).\(\dfrac{25}{3}\)
=>CD=\(\dfrac{20\sqrt{3}}{3}\)(cm)
b/xét △AHC vuông tại H, có HE là đường cao, ta có:
AH²=CE.CA(HTL)(1)
xét △DHC vuông tại H, có HF là đường cao, ta có:

AH²=CF.CD(HTL)(2)
từ (1)và(2), ta suy ra:CF.CD=CE.CA
c/Ta có:AB+BC=8(cm)

=>BC=8-AB(cm)
Diện tích △ABC là:

S_△ABC=\(\dfrac{BC.AH}{2}\)=\(\dfrac{\left(8-AB\right).3}{2}\)
(làm dc tới đây thoiii)