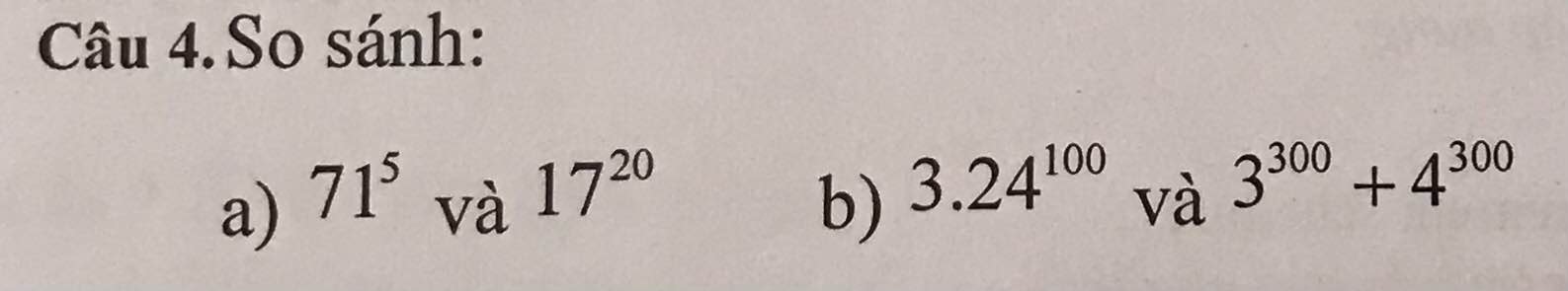Question

Answer 1

a) Ta có: \(17^{20}=\left(17^2\right)^{10}=289^{10}>71^{10}>71^5\)

b) \(3.24^{100}=3.3^{100}.8^{100}=3^{101}.2^{300}\)

\(4^{300}=2^{300}.2^{300}=4^{150}.2^{300}\)

Vì \(3^{101}.2^{300}< 4^{150}.2^{300}\Rightarrow3.24^{100}< 4^{300}\Rightarrow3.24^{100}< 3^{300}+4^{300}\)

Answer 2

a: Ta có: \(17^{20}=\left(17^4\right)^5=83521^5\)

mà \(71< 83521\)

nên \(71^5< 17^{20}\)