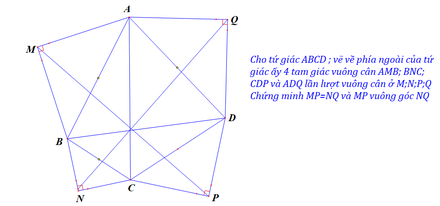
Bài 4:
a) Kẻ đường cao MH
Xét tứ giác MNHQ có
\(\widehat{NMQ}=90^0\)
\(\widehat{NHQ}=90^0\)
\(\widehat{MQH}=90^0\)
Do đó: MNHQ là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
mà MN=MQ(gt)
nên MNHQ là hình vuông(Dấu hiệu nhận biết hình vuông)
Suy ra: \(\widehat{MNH}=90^0\) và NH=QH=MQ
mà \(MQ=\dfrac{1}{2}QP\)
nên \(QH=NH=\dfrac{1}{2}QP\)
hay H là trung điểm của QP
Xét ΔNQP có
NH là đường cao ứng với cạnh QP(gt)
NH là đường trung tuyến ứng với cạnh QP(cmt)
Do đó: ΔNQP cân tại N(Định lí tam giác cân)
Xét ΔNQP cân tại N có
NH là đường trung tuyến ứng với cạnh QP(cmt)
\(NH=\dfrac{QP}{2}\)(cmt)
Do đó: ΔNQP vuông cân tại N(Định lí 2 về áp dụng hình chữ nhật vào tam giác vuông)